an encyclopedia of finite element definitions
Argyris
Click here to read what the information on this page means.
| Degrees | \(5\leqslant k\) where \(k\) is the polynomial subdegree |
| Polynomial subdegree | \(k\) |
| Polynomial superdegree | \(k\) |
| Reference cells | triangle |
| Finite dimensional space | \(\mathcal{P}_{k}\) ↓ Show set definitions ↓ |
| DOFs | On each vertex: point evaluations, point evaluations of first derivatives, and point evaluations of second derivatives On each edge: normal derivative integral moments with a degree \(k-5\) Lagrange space, and integral moments with a degree \(k-6\) Lagrange space On each face: integral moments with a degree \(k-6\) Lagrange space |
| Number of DOFs | triangle: \(21+6(k-5)+(k-5)(k-4)/2\) |
| Mapping | see [2] |
| continuity | Function values and derivatives are continuous. |
| Categories | Scalar-valued elements |
Implementations
This element is implemented in FIAT and Symfem .↓ Show implementation detail ↓Examples
| triangle degree 5 | 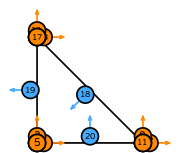 (click to view basis functions) |
References
- [1] Argyris, John H., Fried, Isaac, and Scharpf, Dieter W. The TUBA family of plate elements for the matrix displacement method, The Aeronautical Journal 72(692), 701–709, 1968. [DOI: 10.1017/S000192400008489X] [BibTeX]
- [2] Kirby, Robert C. A general approach to transforming finite elements, The SMAI journal of computational mathematics 4, 197–224, 2018. [DOI: 10.5802/smai-jcm.33] [BibTeX]
DefElement stats
| Element added | 09 January 2021 |
| Element last updated | 20 November 2025 |