an encyclopedia of finite element definitions

Bernstein

Click here to read what the information on this page means.

Alternative names	Bernstein–Bézier
Degrees	\(0\leqslant k\) where \(k\) is the polynomial subdegree
Polynomial subdegree	\(k\)
Polynomial superdegree	\(k\)
Reference cells	interval, triangle, tetrahedron
Finite dimensional space	\(\mathcal{P}_{k}\) ↓ Show set definitions ↓↑ Hide set definitions ↑ \(\mathcal{P}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle\|\sum_{i=1}^dp_i\leqslant k\right\}\)
DOFs	On each vertex: point evaluations On each edge: evaluation of Bernstein coefficients On each face: evaluation of Bernstein coefficients On each volume: evaluation of Bernstein coefficients
Number of DOFs	interval: \(k+1\) (A000027) triangle: \((k+1)(k+2)/2\) (A000217) tetrahedron: \((k+1)(k+2)(k+3)/6\) (A000292)
Mapping	identity
continuity	Function values are continuous.
Categories	Scalar-valued elements

Implementations

This element is implemented in Basix.UFL, FIAT , and Symfem .↓ Show implementation detail ↓

↑ Hide implementation detail ↑

Basix.UFL	Uses custom element code ↓ Show Basix.UFL examples ↓↑ Hide Basix.UFL examples ↑ Before running this example, you must install Basix.UFL: pip3 install git+https://github.com/FEniCS/basix fenics-ufl This element can then be created with the following lines of Python: import basix import basix.ufl import numpy as np # Create Bernstein degree 1 on a interval e = basix.ufl.custom_element( basix.CellType.interval, (), np.array([[1.0, 0.0], [0.5, 0.2886751345948128]], dtype=np.float64), [[np.array([[0.0]], dtype=np.float64), np.array([[1.0]], dtype=np.float64)], [np.empty((0, 1), dtype=np.float64)], [], []], [[np.array([[[[1.0]]]], dtype=np.float64), np.array([[[[1.0]]]], dtype=np.float64)], [np.empty((0, 1, 0, 1), dtype=np.float64)], [], []], 0, basix.MapType.identity, basix.SobolevSpace.H1, False, -1, 1, basix.PolysetType.standard, dtype=np.float64 ) # Create Bernstein degree 2 on a interval e = basix.ufl.custom_element( basix.CellType.interval, (), np.array([[0.9999999999999998, 0.0, 0.0], [0.4999999999999999, 0.28867513459481275, 0.0], [0.33333333333333326, 0.2886751345948128, 0.074535599249993]], dtype=np.float64), [[np.array([[0.0]], dtype=np.float64), np.array([[1.0]], dtype=np.float64)], [np.array([[0.1127016653792583], [0.5], [0.8872983346207417]], dtype=np.float64)], [], []], [[np.array([[[[1.0]]]], dtype=np.float64), np.array([[[[1.0]]]], dtype=np.float64)], [np.array([[[[-0.8333333333333335], [2.6666666666666665], [-0.8333333333333335]]]], dtype=np.float64)], [], []], 0, basix.MapType.identity, basix.SobolevSpace.H1, False, -1, 2, basix.PolysetType.standard, dtype=np.float64 ) # Create Bernstein degree 3 on a interval e = basix.ufl.custom_element( basix.CellType.interval, (), np.array([[0.9999999999999998, -1.1102230246251565e-16, -3.885780586188048e-16, -1.942890293094024e-16], [0.4999999999999999, 0.2886751345948127, -2.7755575615628914e-16, -3.3306690738754696e-16], [0.33333333333333326, 0.2886751345948127, 0.07453559924999278, -3.469446951953614e-16], [0.2499999999999999, 0.2598076211353314, 0.11180339887498926, 0.018898223650461038]], dtype=np.float64), [[np.array([[0.0]], dtype=np.float64), np.array([[1.0]], dtype=np.float64)], [np.array([[0.06943184420297371], [0.33000947820757187], [0.6699905217924281], [0.9305681557970262]], dtype=np.float64)], [], []], [[np.array([[[[1.0]]]], dtype=np.float64), np.array([[[[1.0]]]], dtype=np.float64)], [np.array([[[[-1.321886410500132], [3.788756525742932], [-2.071595286842562], [0.6047251715997604]]], [[[0.6047251715997631], [-2.071595286842563], [3.788756525742931], [-1.321886410500129]]]], dtype=np.float64)], [], []], 0, basix.MapType.identity, basix.SobolevSpace.H1, False, -1, 3, basix.PolysetType.standard, dtype=np.float64 ) # 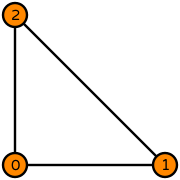Create Bernstein degree 1 on a triangle e = basix.ufl.custom_element( basix.CellType.triangle, (), np.array([[0.7071067811865475, -5.551115123125783e-17, -1.6653345369377348e-16], [0.23570226039551584, -0.08333333333333334, 0.14433756729740632], [0.2357022603955158, 0.16666666666666657, -6.245004513516506e-17]], dtype=np.float64), [[np.array([[0.0, 0.0]], dtype=np.float64), np.array([[1.0, 0.0]], dtype=np.float64), np.array([[0.0, 1.0]], dtype=np.float64)], [np.empty((0, 2), dtype=np.float64), np.empty((0, 2), dtype=np.float64), np.empty((0, 2), dtype=np.float64)], [np.empty((0, 2), dtype=np.float64)], []], [[np.array([[[[1.0]]]], dtype=np.float64), np.array([[[[1.0]]]], dtype=np.float64), np.array([[[[1.0]]]], dtype=np.float64)], [np.empty((0, 1, 0, 1), dtype=np.float64), np.empty((0, 1, 0, 1), dtype=np.float64), np.empty((0, 1, 0, 1), dtype=np.float64)], [np.empty((0, 1, 0, 1), dtype=np.float64)], []], 0, basix.MapType.identity, basix.SobolevSpace.H1, False, -1, 1, basix.PolysetType.standard, dtype=np.float64 ) # 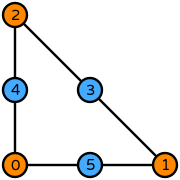Create Bernstein degree 2 on a triangle e = basix.ufl.custom_element( basix.CellType.triangle, (), np.array([[0.7071067811865469, 3.0531133177191805e-16, 5.551115123125783e-16, 1.2490009027033011e-15, 4.718447854656915e-16, 1.5421691701433815e-15], [0.23570226039551567, -0.08333333333333331, 0.1443375672974068, 3.0531133177191805e-16, 1.3877787807814457e-17, 1.1518563880486e-15], [0.11785113019775795, -0.06666666666666671, 0.11547005383792548, 0.013608276348795474, -0.023570226039551674, 0.030429030972510054], [0.2357022603955157, 0.16666666666666693, 1.8735013540549517e-16, 9.43689570931383e-16, 5.689893001203927e-16, 4.475586568020162e-16], [0.05892556509887891, 0.01666666666666671, 0.02886751345948136, -0.02041241452319297, 0.023570226039551632, 2.0643209364124004e-16], [0.11785113019775793, 0.13333333333333364, 1.2836953722228372e-16, 0.04082482904638697, 4.787836793695988e-16, 1.3964523981613297e-16]], dtype=np.float64), [[np.array([[0.0, 0.0]], dtype=np.float64), np.array([[1.0, 0.0]], dtype=np.float64), np.array([[0.0, 1.0]], dtype=np.float64)], [np.array([[0.8872983346207417, 0.1127016653792583], [0.5, 0.5], [0.1127016653792583, 0.8872983346207417]], dtype=np.float64), np.array([[0.0, 0.1127016653792583], [0.0, 0.5], [0.0, 0.8872983346207417]], dtype=np.float64), np.array([[0.1127016653792583, 0.0], [0.5, 0.0], [0.8872983346207417, 0.0]], dtype=np.float64)], [np.empty((0, 2), dtype=np.float64)], []], [[np.array([[[[1.0]]]], dtype=np.float64), np.array([[[[1.0]]]], dtype=np.float64), np.array([[[[1.0]]]], dtype=np.float64)], [np.array([[[[-0.5892556509887897], [1.8856180831641265], [-0.5892556509887897]]]], dtype=np.float64), np.array([[[[-0.8333333333333335], [2.6666666666666665], [-0.8333333333333335]]]], dtype=np.float64), np.array([[[[-0.8333333333333335], [2.6666666666666665], [-0.8333333333333335]]]], dtype=np.float64)], [np.empty((0, 1, 0, 1), dtype=np.float64)], []], 0, basix.MapType.identity, basix.SobolevSpace.H1, False, -1, 2, basix.PolysetType.standard, dtype=np.float64 ) # 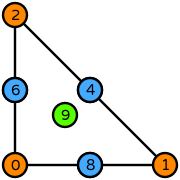Create Bernstein degree 3 on a triangle e = basix.ufl.custom_element( basix.CellType.triangle, (), np.array([[0.7071067811865489, -3.608224830031759e-16, -5.967448757360216e-16, 3.434752482434078e-15, -4.926614671774132e-16, 2.67841304690819e-15, -3.2335245592207684e-15, 3.191891195797325e-16, 7.896461262646426e-15, 4.649058915617843e-16], [0.23570226039551628, -0.08333333333333401, 0.14433756729740724, 1.40989650510015e-15, 3.0357660829594124e-16, 6.557254739192331e-16, -1.7403613272737317e-15, 7.485331798839923e-16, 2.4060614611798314e-15, 1.0174153186603974e-15], [0.11785113019775828, -0.06666666666666712, 0.11547005383792579, 0.01360827634879615, -0.023570226039551643, 0.030429030972509735, -9.993633524885137e-16, 5.049671618351237e-16, 1.0830908652587068e-15, 6.541533807691291e-16], [0.07071067811865506, -0.05000000000000034, 0.08660254037844436, 0.01749635530559457, -0.030304576336566497, 0.03912303982179802, -0.0025253813613811296, 0.0043740888263988946, -0.005646924393157328, 0.006681531047811082], [0.23570226039551628, 0.1666666666666677, -2.0469737016526324e-16, 7.667477763817487e-16, -2.255140518769849e-16, 1.349614864309956e-15, 1.4051260155412137e-16, 5.898059818321144e-17, 3.226585665316861e-15, 1.6306400674181987e-16], [0.05892556509887893, 0.016666666666666784, 0.028867513459481495, -0.020412414523193062, 0.02357022603955198, 3.8510861166685117e-16, -1.0592655225183378e-16, 2.205267218835516e-16, 8.020927672047762e-16, 3.2482697087665713e-16], [0.023570226039551605, 5.648608615354753e-17, 0.019245008972987636, -0.009720197391996737, 0.01010152544552229, 0.004347004424644381, 0.0033671751485073037, -0.004860098695998318, 0.00376461626210557, 2.0734011296069665e-16], [0.1178511301977583, 0.1333333333333341, -7.632783294297951e-17, 0.04082482904638698, -1.0495077029659683e-16, 5.872038966181492e-16, 3.616898447411643e-16, 5.204170427930421e-18, 1.6705387073656652e-15, 5.941427905220564e-17], [0.0235702260395516, 0.01666666666666674, 0.009622504486493866, -0.005832118435197997, 0.0134687005940297, 1.537940781670688e-16, -0.005050762722761071, 0.004860098695998528, 3.7925391993542945e-16, 1.0527603094834248e-16], [0.07071067811865506, 0.1000000000000006, -3.252606517456513e-17, 0.052489065916782984, -4.96564594998361e-17, 2.894819800536297e-16, 0.010101525445522504, -2.168404344971009e-18, 9.341485918135106e-16, 2.5478751053409354e-17]], dtype=np.float64), [[np.array([[0.0, 0.0]], dtype=np.float64), np.array([[1.0, 0.0]], dtype=np.float64), np.array([[0.0, 1.0]], dtype=np.float64)], [np.array([[0.9305681557970262, 0.06943184420297371], [0.6699905217924281, 0.33000947820757187], [0.33000947820757187, 0.6699905217924281], [0.06943184420297377, 0.9305681557970262]], dtype=np.float64), np.array([[0.0, 0.06943184420297371], [0.0, 0.33000947820757187], [0.0, 0.6699905217924281], [0.0, 0.9305681557970262]], dtype=np.float64), np.array([[0.06943184420297371, 0.0], [0.33000947820757187, 0.0], [0.6699905217924281, 0.0], [0.9305681557970262, 0.0]], dtype=np.float64)], [np.array([[0.873821971016996, 0.063089014491502], [0.063089014491502, 0.873821971016996], [0.063089014491502, 0.063089014491502], [0.501426509658179, 0.24928674517091], [0.24928674517091, 0.501426509658179], [0.24928674517091, 0.24928674517091], [0.636502499121399, 0.310352451033785], [0.636502499121399, 0.053145049844816], [0.310352451033785, 0.636502499121399], [0.310352451033785, 0.053145049844816], [0.053145049844816, 0.636502499121399], [0.053145049844816, 0.310352451033785]], dtype=np.float64)], []], [[np.array([[[[1.0]]]], dtype=np.float64), np.array([[[[1.0]]]], dtype=np.float64), np.array([[[[1.0]]]], dtype=np.float64)], [np.array([[[[-0.9347148448229876], [2.679055431617612], [-1.4648390752004665], [0.4276052695923897]]], [[[0.42760526959239115], [-1.4648390752004672], [2.679055431617611], [-0.9347148448229856]]]], dtype=np.float64), np.array([[[[-1.321886410500132], [3.788756525742932], [-2.071595286842562], [0.6047251715997604]]], [[[0.6047251715997631], [-2.071595286842563], [3.788756525742931], [-1.321886410500129]]]], dtype=np.float64), np.array([[[[-1.321886410500132], [3.788756525742932], [-2.071595286842562], [0.6047251715997604]]], [[[0.6047251715997631], [-2.071595286842563], [3.788756525742931], [-1.321886410500129]]]], dtype=np.float64)], [np.array([[[[0.6969012929501789], [0.6969012929501781], [0.6969012929501789], [2.756156721047493], [2.7561567210474927], [2.75615672104748], [-1.5598623403322074], [-1.5598623403322096], [-1.559862340332209], [-1.5598623403322098], [-1.55986234033221], [-1.559862340332211]]]], dtype=np.float64)], []], 0, basix.MapType.identity, basix.SobolevSpace.H1, False, -1, 3, basix.PolysetType.standard, dtype=np.float64 )
FIAT	`FIAT.Bernstein` ↓ Show FIAT examples ↓↑ Hide FIAT examples ↑ Before running this example, you must install FIAT: pip3 install git+https://github.com/firedrakeproject/fiat.git This element can then be created with the following lines of Python: import FIAT # Create Bernstein degree 1 element = FIAT.Bernstein(FIAT.ufc_cell("interval"), 1) # Create Bernstein degree 2 element = FIAT.Bernstein(FIAT.ufc_cell("interval"), 2) # Create Bernstein degree 3 element = FIAT.Bernstein(FIAT.ufc_cell("interval"), 3) # Create Bernstein degree 1 element = FIAT.Bernstein(FIAT.ufc_cell("triangle"), 1) # Create Bernstein degree 2 element = FIAT.Bernstein(FIAT.ufc_cell("triangle"), 2) # Create Bernstein degree 3 element = FIAT.Bernstein(FIAT.ufc_cell("triangle"), 3) This implementation is correct for all the examples below.
Symfem	`"Bernstein"` ↓ Show Symfem examples ↓↑ Hide Symfem examples ↑ Before running this example, you must install Symfem: pip3 install symfem This element can then be created with the following lines of Python: import symfem # Create Bernstein degree 1 on a interval element = symfem.create_element("interval", "Bernstein", 1) # Create Bernstein degree 2 on a interval element = symfem.create_element("interval", "Bernstein", 2) # Create Bernstein degree 3 on a interval element = symfem.create_element("interval", "Bernstein", 3) # Create Bernstein degree 1 on a triangle element = symfem.create_element("triangle", "Bernstein", 1) # Create Bernstein degree 2 on a triangle element = symfem.create_element("triangle", "Bernstein", 2) # Create Bernstein degree 3 on a triangle element = symfem.create_element("triangle", "Bernstein", 3) This implementation is used to compute the examples below and verify other implementations.

Examples

interval degree 1	(click to view basis functions)
interval degree 2	(click to view basis functions)
interval degree 3	(click to view basis functions)
triangle degree 1	(click to view basis functions)
triangle degree 2	(click to view basis functions)
triangle degree 3	(click to view basis functions)

References

[1] Ainsworth, Mark, Andriamaro, Gaelle, and Davydov, Oleg. Bernstein–Bézier finite elements of arbitrary order and optimal assembly procedures, SIAM Journal on Scientific Computing 33(6), 3087–3109, 2011. [DOI: 10.1137/11082539X] [BibTeX]
[2] Kirby, Robert C. Fast simplicial finite element algorithms using Bernstein polynomials, Numerische Mathematik 117(4), 631–652, 2011. [DOI: 10.1007/s00211-010-0327-2] [BibTeX]

DefElement stats

Element added	20 February 2021
Element last updated	17 November 2025