Click here to read what the information on this page means.
| Degrees | interval: \(2\leqslant k\)
triangle: \(3\leqslant k\)
tetrahedron: \(4\leqslant k\)
where \(k\) is the polynomial superdegree |
| Polynomial subdegree | \(-1\) |
| Polynomial superdegree | interval: \(k\)
triangle: \(k\)
tetrahedron: \(k\)
quadrilateral: \(dk\)
hexahedron: \(dk\) |
| Reference cells | interval, triangle, tetrahedron |
| Finite dimensional space | \(\mathcal{Z}^{(11)}_{k}\)
↓ Show set definitions ↓↑ Hide set definitions ↑\(\mathcal{Z}^{(11)}_k=\left\{p\in \mathcal{P}_{k}\middle|p=0\text{ on the boundary}\right\}\)
\(\mathcal{P}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle|\sum_{i=1}^dp_i\leqslant k\right\}\) |
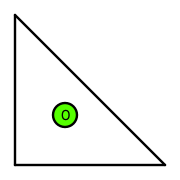
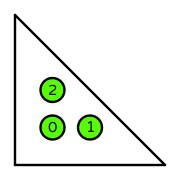
| DOFs | On the interior of the reference cell: point evaluations |
| Number of DOFs | interval: \(k-1\) (A000027)
triangle: \((k-2)(k-1)/2\) (A000217)
tetrahedron: \((k-3)(k-2)(k-1)/6\) (A000292) |
| Mapping | identity |
| continuity | Function values are continuous. |
| Categories | Scalar-valued elements |
This element is implemented in
Basix ,
Basix.UFL ,
FIAT , and
Symfem .
↓ Show implementation detail ↓↑ Hide implementation detail ↑| Basix | basix.ElementFamily.bubble
↓ Show Basix examples ↓↑ Hide Basix examples ↑Before running this example, you must install Basix: pip3 install fenics-basix This element can then be created with the following lines of Python: import basix
# Create bubble degree 2 on a interval
element = basix.create_element(basix.ElementFamily.bubble, basix.CellType.interval, 2)
# Create bubble degree 3 on a interval
element = basix.create_element(basix.ElementFamily.bubble, basix.CellType.interval, 3)
# Create bubble degree 3 on a triangle
element = basix.create_element(basix.ElementFamily.bubble, basix.CellType.triangle, 3)
# Create bubble degree 4 on a triangle
element = basix.create_element(basix.ElementFamily.bubble, basix.CellType.triangle, 4) |
| Basix.UFL | basix.ElementFamily.bubble
↓ Show Basix.UFL examples ↓↑ Hide Basix.UFL examples ↑Before running this example, you must install Basix.UFL: pip3 install git+https://github.com/FEniCS/basix fenics-ufl This element can then be created with the following lines of Python: import basix
import basix.ufl
# Create bubble degree 2 on a interval
element = basix.ufl.element(basix.ElementFamily.bubble, basix.CellType.interval, 2)
# Create bubble degree 3 on a interval
element = basix.ufl.element(basix.ElementFamily.bubble, basix.CellType.interval, 3)
# Create bubble degree 3 on a triangle
element = basix.ufl.element(basix.ElementFamily.bubble, basix.CellType.triangle, 3)
# Create bubble degree 4 on a triangle
element = basix.ufl.element(basix.ElementFamily.bubble, basix.CellType.triangle, 4) |
| FIAT | FIAT.Bubble
↓ Show FIAT examples ↓↑ Hide FIAT examples ↑Before running this example, you must install FIAT: pip3 install git+https://github.com/firedrakeproject/fiat.git This element can then be created with the following lines of Python: import FIAT
# Create bubble degree 2
element = FIAT.Bubble(FIAT.ufc_cell("interval"), 2)
# Create bubble degree 3
element = FIAT.Bubble(FIAT.ufc_cell("interval"), 3)
# Create bubble degree 3
element = FIAT.Bubble(FIAT.ufc_cell("triangle"), 3)
# Create bubble degree 4
element = FIAT.Bubble(FIAT.ufc_cell("triangle"), 4) |
| Symfem | "bubble"
↓ Show Symfem examples ↓↑ Hide Symfem examples ↑Before running this example, you must install Symfem: pip3 install symfem This element can then be created with the following lines of Python: import symfem
# Create bubble degree 2 on a interval
element = symfem.create_element("interval", "bubble", 2)
# Create bubble degree 3 on a interval
element = symfem.create_element("interval", "bubble", 3)
# Create bubble degree 3 on a triangle
element = symfem.create_element("triangle", "bubble", 3)
# Create bubble degree 4 on a triangle
element = symfem.create_element("triangle", "bubble", 4) |
- [1] Kirby, Robert C., Logg, Anders, Rognes, Marie E., and Terrel, Andy R. Common and unusual finite elements, in Automated solution of differential equations by the finite element method (eds: Logg, Anders, Mardal, Kent-Andre, and Wells, Garth N.), 95–119, 2012. [DOI: 10.1007/978-3-642-23099-8_3] [BibTeX]
| Element added | 10 January 2021 |
| Element last updated | 17 November 2025 |
