an encyclopedia of finite element definitions
Enriched Galerkin
Click here to read what the information on this page means.
| Abbreviated names | EG |
| Degrees | \(1\leqslant k\) where \(k\) is the Polynomial subdegree |
| Polynomial subdegree | \(k\) |
| Polynomial superdegree | interval: \(k\) triangle: \(k\) tetrahedron: \(k\) quadrilateral: \(dk\) hexahedron: \(dk\) |
| Lagrange subdegree | \(k\) |
| Lagrange superdegree | \(k\) |
| Reference elements | interval, triangle, tetrahedron, quadrilateral, hexahedron, prism, pyramid |
| Number of DOFs | interval: \(k+2\) (A000027) triangle: \((k+1)(k+2)/2 + 1\) tetrahedron: \((k+1)(k+2)(k+3)/6 + 1\) quadrilateral: \((k+1)^2 + 1\) hexahedron: \((k+1)^3 + 1\) prism: \((k+1)^2(k+2)/2 + 1\) pyramid: \((k+1)(k+2)(2k+3)/6 + 1\) |
| Mapping | identity |
| continuity | Discontinuous. |
| Notes | This is a continuous Lagrange element enriched with a discontinuous piecewise constant element. |
| Categories | Scalar-valued elements |
Implementations
This element is implemented in Symfem .↓ Show implementation detail ↓Examples
| interval degree 1 |  (click to view basis functions) |
| interval degree 2 |  (click to view basis functions) |
| triangle degree 1 | 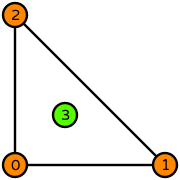 (click to view basis functions) |
| triangle degree 2 | 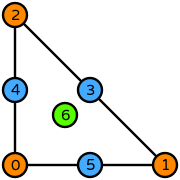 (click to view basis functions) |
| quadrilateral degree 1 | 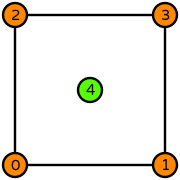 (click to view basis functions) |
| quadrilateral degree 2 |  (click to view basis functions) |
| tetrahedron degree 1 | 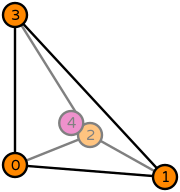 (click to view basis functions) |
| tetrahedron degree 2 | 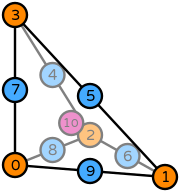 (click to view basis functions) |
| hexahedron degree 1 | 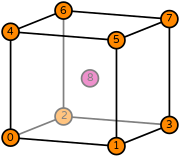 (click to view basis functions) |
| hexahedron degree 2 | 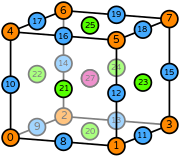 (click to view basis functions) |
References
- Becker, Roland, Burman, Erik, Hansbo, Peter, and Larson, Mats G. A reduced P1-discontinuous Galerkin method, Chalmers Finite Element Center Preprint 2003-13, Chalmers University of Technology, Göteborg, Sweden,, 2003. [BibTeX]
DefElement stats
| Element added | 05 March 2023 |
| Element last updated | 11 April 2025 |