Degree 1 P1-iso-P2 on a interval

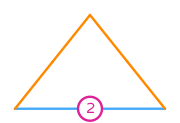
• \(R\) is the reference interval. The following numbering of the subentities of the reference is used:

• \(\mathcal{V}\) is spanned by: \(\begin{cases} 1 - 2 x&\text{in }\operatorname{Interval}(((0,), (1/2,)))\\0&\text{in }\operatorname{Interval}(((1/2,), (1,)))\end{cases}\), \(\begin{cases} 2 x&\text{in }\operatorname{Interval}(((0,), (1/2,)))\\2 - 2 x&\text{in }\operatorname{Interval}(((1/2,), (1,)))\end{cases}\), \(\begin{cases} 0&\text{in }\operatorname{Interval}(((0,), (1/2,)))\\2 x - 1&\text{in }\operatorname{Interval}(((1/2,), (1,)))\end{cases}\)
• \(\mathcal{L}=\{l_0,...,l_{2}\}\)
• Functionals and basis functions:

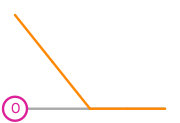
\(\displaystyle l_{0}:v\mapsto v(0)\)

\(\displaystyle \phi_{0} = \begin{cases} 1 - 2 x&\text{in }\operatorname{Interval}(((0,), (1/2,)))\\0&\text{in }\operatorname{Interval}(((1/2,), (1,)))\end{cases}\)

This DOF is associated with vertex 0 of the reference element.

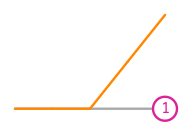
\(\displaystyle l_{1}:v\mapsto v(1)\)

\(\displaystyle \phi_{1} = \begin{cases} 0&\text{in }\operatorname{Interval}(((0,), (1/2,)))\\2 x - 1&\text{in }\operatorname{Interval}(((1/2,), (1,)))\end{cases}\)

This DOF is associated with vertex 1 of the reference element.

\(\displaystyle l_{2}:v\mapsto v(\tfrac{1}{2})\)

\(\displaystyle \phi_{2} = \begin{cases} 2 x&\text{in }\operatorname{Interval}(((0,), (1/2,)))\\2 - 2 x&\text{in }\operatorname{Interval}(((1/2,), (1,)))\end{cases}\)

This DOF is associated with edge 0 of the reference element.