an encyclopedia of finite element definitions
Degree 2 Tiniest tensor H(curl) on a quadrilateral
◀ Back to Tiniest tensor H(curl) definition page
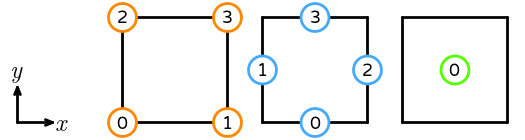
- \(R\) is the reference quadrilateral. The following numbering of the sub-entities of the reference cell is used:
- \(\mathcal{V}\) is spanned by: \(\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle y\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle y\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle y^{2}\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle y^{2}\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle x\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle x\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle x y\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle x y\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle x y^{2}\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle x y^{2}\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle x^{2}\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle x^{2}\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle x^{2} y\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle x^{2} y\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle x^{2} y^{2}\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle x^{2} y^{2}\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 2 y \left(2 y^{2} - 3 y + 1\right)\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 2 x \left(- 2 x^{2} + 3 x - 1\right)\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 2 y \left(12 x^{2} y^{2} - 18 x^{2} y + 6 x^{2} - 12 x y^{2} + 18 x y - 6 x + 2 y^{2} - 3 y + 1\right)\\\displaystyle 2 x \left(- 12 x^{2} y^{2} + 12 x^{2} y - 2 x^{2} + 18 x y^{2} - 18 x y + 3 x - 6 y^{2} + 6 y - 1\right)\end{array}\right)\)
- \(\mathcal{L}=\{l_0,...,l_{20}\}\)
- Functionals and basis functions:
\(\displaystyle l_{0}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{0}}\boldsymbol{v}\cdot(2 s_{0}^{2} - 3 s_{0} + 1)\hat{\boldsymbol{t}}_{0}\)
where \(e_{0}\) is the 0th edge;
\(\hat{\boldsymbol{t}}_{0}\) is the tangent to edge 0;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \boldsymbol{\phi}_{0} = \left(\begin{array}{c}\displaystyle - 150 x^{2} y^{3} + 315 x^{2} y^{2} - 195 x^{2} y + 30 x^{2} + 150 x y^{3} - \frac{663 x y^{2}}{2} + \frac{435 x y}{2} - 36 x - 35 y^{3} + \frac{315 y^{2}}{4} - \frac{211 y}{4} + 9\\\displaystyle \frac{x \left(600 x^{2} y^{2} - 600 x^{2} y + 100 x^{2} - 1260 x y^{2} + 1266 x y - 213 x + 660 y^{2} - 666 y + 113\right)}{4}\end{array}\right)\)
This DOF is associated with edge 0 of the reference cell.
where \(e_{0}\) is the 0th edge;
\(\hat{\boldsymbol{t}}_{0}\) is the tangent to edge 0;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \boldsymbol{\phi}_{0} = \left(\begin{array}{c}\displaystyle - 150 x^{2} y^{3} + 315 x^{2} y^{2} - 195 x^{2} y + 30 x^{2} + 150 x y^{3} - \frac{663 x y^{2}}{2} + \frac{435 x y}{2} - 36 x - 35 y^{3} + \frac{315 y^{2}}{4} - \frac{211 y}{4} + 9\\\displaystyle \frac{x \left(600 x^{2} y^{2} - 600 x^{2} y + 100 x^{2} - 1260 x y^{2} + 1266 x y - 213 x + 660 y^{2} - 666 y + 113\right)}{4}\end{array}\right)\)
This DOF is associated with edge 0 of the reference cell.
\(\displaystyle l_{1}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{0}}\boldsymbol{v}\cdot(s_{0} \left(2 s_{0} - 1\right))\hat{\boldsymbol{t}}_{0}\)
where \(e_{0}\) is the 0th edge;
\(\hat{\boldsymbol{t}}_{0}\) is the tangent to edge 0;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \boldsymbol{\phi}_{1} = \left(\begin{array}{c}\displaystyle - 150 x^{2} y^{3} + 315 x^{2} y^{2} - 195 x^{2} y + 30 x^{2} + 150 x y^{3} - \frac{597 x y^{2}}{2} + \frac{345 x y}{2} - 24 x - 35 y^{3} + \frac{249 y^{2}}{4} - \frac{121 y}{4} + 3\\\displaystyle \frac{x \left(600 x^{2} y^{2} - 600 x^{2} y + 100 x^{2} - 540 x y^{2} + 534 x y - 87 x - 60 y^{2} + 66 y - 13\right)}{4}\end{array}\right)\)
This DOF is associated with edge 0 of the reference cell.
where \(e_{0}\) is the 0th edge;
\(\hat{\boldsymbol{t}}_{0}\) is the tangent to edge 0;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \boldsymbol{\phi}_{1} = \left(\begin{array}{c}\displaystyle - 150 x^{2} y^{3} + 315 x^{2} y^{2} - 195 x^{2} y + 30 x^{2} + 150 x y^{3} - \frac{597 x y^{2}}{2} + \frac{345 x y}{2} - 24 x - 35 y^{3} + \frac{249 y^{2}}{4} - \frac{121 y}{4} + 3\\\displaystyle \frac{x \left(600 x^{2} y^{2} - 600 x^{2} y + 100 x^{2} - 540 x y^{2} + 534 x y - 87 x - 60 y^{2} + 66 y - 13\right)}{4}\end{array}\right)\)
This DOF is associated with edge 0 of the reference cell.
\(\displaystyle l_{2}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{0}}\boldsymbol{v}\cdot(4 s_{0} \left(1 - s_{0}\right))\hat{\boldsymbol{t}}_{0}\)
where \(e_{0}\) is the 0th edge;
\(\hat{\boldsymbol{t}}_{0}\) is the tangent to edge 0;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \boldsymbol{\phi}_{2} = \left(\begin{array}{c}\displaystyle 75 x^{2} y^{3} - \frac{315 x^{2} y^{2}}{2} + \frac{195 x^{2} y}{2} - 15 x^{2} - 75 x y^{3} + \frac{315 x y^{2}}{2} - \frac{195 x y}{2} + 15 x + \frac{5 y^{3}}{2} - \frac{33 y^{2}}{4} + \frac{29 y}{4} - \frac{3}{2}\\\displaystyle \frac{25 x \left(- 12 x^{2} y^{2} + 12 x^{2} y - 2 x^{2} + 18 x y^{2} - 18 x y + 3 x - 6 y^{2} + 6 y - 1\right)}{4}\end{array}\right)\)
This DOF is associated with edge 0 of the reference cell.
where \(e_{0}\) is the 0th edge;
\(\hat{\boldsymbol{t}}_{0}\) is the tangent to edge 0;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \boldsymbol{\phi}_{2} = \left(\begin{array}{c}\displaystyle 75 x^{2} y^{3} - \frac{315 x^{2} y^{2}}{2} + \frac{195 x^{2} y}{2} - 15 x^{2} - 75 x y^{3} + \frac{315 x y^{2}}{2} - \frac{195 x y}{2} + 15 x + \frac{5 y^{3}}{2} - \frac{33 y^{2}}{4} + \frac{29 y}{4} - \frac{3}{2}\\\displaystyle \frac{25 x \left(- 12 x^{2} y^{2} + 12 x^{2} y - 2 x^{2} + 18 x y^{2} - 18 x y + 3 x - 6 y^{2} + 6 y - 1\right)}{4}\end{array}\right)\)
This DOF is associated with edge 0 of the reference cell.
\(\displaystyle l_{3}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{1}}\boldsymbol{v}\cdot(2 s_{0}^{2} - 3 s_{0} + 1)\hat{\boldsymbol{t}}_{1}\)
where \(e_{1}\) is the 1st edge;
\(\hat{\boldsymbol{t}}_{1}\) is the tangent to edge 1;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \boldsymbol{\phi}_{3} = \left(\begin{array}{c}\displaystyle \frac{y \left(600 x^{2} y^{2} - 1260 x^{2} y + 660 x^{2} - 600 x y^{2} + 1266 x y - 666 x + 100 y^{2} - 213 y + 113\right)}{4}\\\displaystyle - 150 x^{3} y^{2} + 150 x^{3} y - 35 x^{3} + 315 x^{2} y^{2} - \frac{663 x^{2} y}{2} + \frac{315 x^{2}}{4} - 195 x y^{2} + \frac{435 x y}{2} - \frac{211 x}{4} + 30 y^{2} - 36 y + 9\end{array}\right)\)
This DOF is associated with edge 1 of the reference cell.
where \(e_{1}\) is the 1st edge;
\(\hat{\boldsymbol{t}}_{1}\) is the tangent to edge 1;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \boldsymbol{\phi}_{3} = \left(\begin{array}{c}\displaystyle \frac{y \left(600 x^{2} y^{2} - 1260 x^{2} y + 660 x^{2} - 600 x y^{2} + 1266 x y - 666 x + 100 y^{2} - 213 y + 113\right)}{4}\\\displaystyle - 150 x^{3} y^{2} + 150 x^{3} y - 35 x^{3} + 315 x^{2} y^{2} - \frac{663 x^{2} y}{2} + \frac{315 x^{2}}{4} - 195 x y^{2} + \frac{435 x y}{2} - \frac{211 x}{4} + 30 y^{2} - 36 y + 9\end{array}\right)\)
This DOF is associated with edge 1 of the reference cell.
\(\displaystyle l_{4}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{1}}\boldsymbol{v}\cdot(s_{0} \left(2 s_{0} - 1\right))\hat{\boldsymbol{t}}_{1}\)
where \(e_{1}\) is the 1st edge;
\(\hat{\boldsymbol{t}}_{1}\) is the tangent to edge 1;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \boldsymbol{\phi}_{4} = \left(\begin{array}{c}\displaystyle \frac{y \left(600 x^{2} y^{2} - 540 x^{2} y - 60 x^{2} - 600 x y^{2} + 534 x y + 66 x + 100 y^{2} - 87 y - 13\right)}{4}\\\displaystyle - 150 x^{3} y^{2} + 150 x^{3} y - 35 x^{3} + 315 x^{2} y^{2} - \frac{597 x^{2} y}{2} + \frac{249 x^{2}}{4} - 195 x y^{2} + \frac{345 x y}{2} - \frac{121 x}{4} + 30 y^{2} - 24 y + 3\end{array}\right)\)
This DOF is associated with edge 1 of the reference cell.
where \(e_{1}\) is the 1st edge;
\(\hat{\boldsymbol{t}}_{1}\) is the tangent to edge 1;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \boldsymbol{\phi}_{4} = \left(\begin{array}{c}\displaystyle \frac{y \left(600 x^{2} y^{2} - 540 x^{2} y - 60 x^{2} - 600 x y^{2} + 534 x y + 66 x + 100 y^{2} - 87 y - 13\right)}{4}\\\displaystyle - 150 x^{3} y^{2} + 150 x^{3} y - 35 x^{3} + 315 x^{2} y^{2} - \frac{597 x^{2} y}{2} + \frac{249 x^{2}}{4} - 195 x y^{2} + \frac{345 x y}{2} - \frac{121 x}{4} + 30 y^{2} - 24 y + 3\end{array}\right)\)
This DOF is associated with edge 1 of the reference cell.
\(\displaystyle l_{5}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{1}}\boldsymbol{v}\cdot(4 s_{0} \left(1 - s_{0}\right))\hat{\boldsymbol{t}}_{1}\)
where \(e_{1}\) is the 1st edge;
\(\hat{\boldsymbol{t}}_{1}\) is the tangent to edge 1;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \boldsymbol{\phi}_{5} = \left(\begin{array}{c}\displaystyle \frac{25 y \left(- 12 x^{2} y^{2} + 18 x^{2} y - 6 x^{2} + 12 x y^{2} - 18 x y + 6 x - 2 y^{2} + 3 y - 1\right)}{4}\\\displaystyle 75 x^{3} y^{2} - 75 x^{3} y + \frac{5 x^{3}}{2} - \frac{315 x^{2} y^{2}}{2} + \frac{315 x^{2} y}{2} - \frac{33 x^{2}}{4} + \frac{195 x y^{2}}{2} - \frac{195 x y}{2} + \frac{29 x}{4} - 15 y^{2} + 15 y - \frac{3}{2}\end{array}\right)\)
This DOF is associated with edge 1 of the reference cell.
where \(e_{1}\) is the 1st edge;
\(\hat{\boldsymbol{t}}_{1}\) is the tangent to edge 1;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \boldsymbol{\phi}_{5} = \left(\begin{array}{c}\displaystyle \frac{25 y \left(- 12 x^{2} y^{2} + 18 x^{2} y - 6 x^{2} + 12 x y^{2} - 18 x y + 6 x - 2 y^{2} + 3 y - 1\right)}{4}\\\displaystyle 75 x^{3} y^{2} - 75 x^{3} y + \frac{5 x^{3}}{2} - \frac{315 x^{2} y^{2}}{2} + \frac{315 x^{2} y}{2} - \frac{33 x^{2}}{4} + \frac{195 x y^{2}}{2} - \frac{195 x y}{2} + \frac{29 x}{4} - 15 y^{2} + 15 y - \frac{3}{2}\end{array}\right)\)
This DOF is associated with edge 1 of the reference cell.
\(\displaystyle l_{6}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{2}}\boldsymbol{v}\cdot(2 s_{0}^{2} - 3 s_{0} + 1)\hat{\boldsymbol{t}}_{2}\)
where \(e_{2}\) is the 2nd edge;
\(\hat{\boldsymbol{t}}_{2}\) is the tangent to edge 2;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \boldsymbol{\phi}_{6} = \left(\begin{array}{c}\displaystyle \frac{y \left(- 600 x^{2} y^{2} + 1260 x^{2} y - 660 x^{2} + 600 x y^{2} - 1254 x y + 654 x - 100 y^{2} + 207 y - 107\right)}{4}\\\displaystyle \frac{x \left(600 x^{2} y^{2} - 600 x^{2} y + 140 x^{2} - 540 x y^{2} + 474 x y - 105 x + 60 y^{2} - 18 y + 1\right)}{4}\end{array}\right)\)
This DOF is associated with edge 2 of the reference cell.
where \(e_{2}\) is the 2nd edge;
\(\hat{\boldsymbol{t}}_{2}\) is the tangent to edge 2;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \boldsymbol{\phi}_{6} = \left(\begin{array}{c}\displaystyle \frac{y \left(- 600 x^{2} y^{2} + 1260 x^{2} y - 660 x^{2} + 600 x y^{2} - 1254 x y + 654 x - 100 y^{2} + 207 y - 107\right)}{4}\\\displaystyle \frac{x \left(600 x^{2} y^{2} - 600 x^{2} y + 140 x^{2} - 540 x y^{2} + 474 x y - 105 x + 60 y^{2} - 18 y + 1\right)}{4}\end{array}\right)\)
This DOF is associated with edge 2 of the reference cell.
\(\displaystyle l_{7}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{2}}\boldsymbol{v}\cdot(s_{0} \left(2 s_{0} - 1\right))\hat{\boldsymbol{t}}_{2}\)
where \(e_{2}\) is the 2nd edge;
\(\hat{\boldsymbol{t}}_{2}\) is the tangent to edge 2;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \boldsymbol{\phi}_{7} = \left(\begin{array}{c}\displaystyle \frac{y \left(- 600 x^{2} y^{2} + 540 x^{2} y + 60 x^{2} + 600 x y^{2} - 546 x y - 54 x - 100 y^{2} + 93 y + 7\right)}{4}\\\displaystyle \frac{x \left(600 x^{2} y^{2} - 600 x^{2} y + 140 x^{2} - 540 x y^{2} + 606 x y - 171 x + 60 y^{2} - 102 y + 43\right)}{4}\end{array}\right)\)
This DOF is associated with edge 2 of the reference cell.
where \(e_{2}\) is the 2nd edge;
\(\hat{\boldsymbol{t}}_{2}\) is the tangent to edge 2;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \boldsymbol{\phi}_{7} = \left(\begin{array}{c}\displaystyle \frac{y \left(- 600 x^{2} y^{2} + 540 x^{2} y + 60 x^{2} + 600 x y^{2} - 546 x y - 54 x - 100 y^{2} + 93 y + 7\right)}{4}\\\displaystyle \frac{x \left(600 x^{2} y^{2} - 600 x^{2} y + 140 x^{2} - 540 x y^{2} + 606 x y - 171 x + 60 y^{2} - 102 y + 43\right)}{4}\end{array}\right)\)
This DOF is associated with edge 2 of the reference cell.
\(\displaystyle l_{8}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{2}}\boldsymbol{v}\cdot(4 s_{0} \left(1 - s_{0}\right))\hat{\boldsymbol{t}}_{2}\)
where \(e_{2}\) is the 2nd edge;
\(\hat{\boldsymbol{t}}_{2}\) is the tangent to edge 2;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \boldsymbol{\phi}_{8} = \left(\begin{array}{c}\displaystyle \frac{25 y \left(12 x^{2} y^{2} - 18 x^{2} y + 6 x^{2} - 12 x y^{2} + 18 x y - 6 x + 2 y^{2} - 3 y + 1\right)}{4}\\\displaystyle \frac{x \left(- 300 x^{2} y^{2} + 300 x^{2} y - 10 x^{2} + 270 x y^{2} - 270 x y - 3 x - 30 y^{2} + 30 y + 7\right)}{4}\end{array}\right)\)
This DOF is associated with edge 2 of the reference cell.
where \(e_{2}\) is the 2nd edge;
\(\hat{\boldsymbol{t}}_{2}\) is the tangent to edge 2;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \boldsymbol{\phi}_{8} = \left(\begin{array}{c}\displaystyle \frac{25 y \left(12 x^{2} y^{2} - 18 x^{2} y + 6 x^{2} - 12 x y^{2} + 18 x y - 6 x + 2 y^{2} - 3 y + 1\right)}{4}\\\displaystyle \frac{x \left(- 300 x^{2} y^{2} + 300 x^{2} y - 10 x^{2} + 270 x y^{2} - 270 x y - 3 x - 30 y^{2} + 30 y + 7\right)}{4}\end{array}\right)\)
This DOF is associated with edge 2 of the reference cell.
\(\displaystyle l_{9}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{3}}\boldsymbol{v}\cdot(2 s_{0}^{2} - 3 s_{0} + 1)\hat{\boldsymbol{t}}_{3}\)
where \(e_{3}\) is the 3rd edge;
\(\hat{\boldsymbol{t}}_{3}\) is the tangent to edge 3;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{3}\).
\(\displaystyle \boldsymbol{\phi}_{9} = \left(\begin{array}{c}\displaystyle \frac{y \left(600 x^{2} y^{2} - 540 x^{2} y + 60 x^{2} - 600 x y^{2} + 474 x y - 18 x + 140 y^{2} - 105 y + 1\right)}{4}\\\displaystyle \frac{x \left(- 600 x^{2} y^{2} + 600 x^{2} y - 100 x^{2} + 1260 x y^{2} - 1254 x y + 207 x - 660 y^{2} + 654 y - 107\right)}{4}\end{array}\right)\)
This DOF is associated with edge 3 of the reference cell.
where \(e_{3}\) is the 3rd edge;
\(\hat{\boldsymbol{t}}_{3}\) is the tangent to edge 3;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{3}\).
\(\displaystyle \boldsymbol{\phi}_{9} = \left(\begin{array}{c}\displaystyle \frac{y \left(600 x^{2} y^{2} - 540 x^{2} y + 60 x^{2} - 600 x y^{2} + 474 x y - 18 x + 140 y^{2} - 105 y + 1\right)}{4}\\\displaystyle \frac{x \left(- 600 x^{2} y^{2} + 600 x^{2} y - 100 x^{2} + 1260 x y^{2} - 1254 x y + 207 x - 660 y^{2} + 654 y - 107\right)}{4}\end{array}\right)\)
This DOF is associated with edge 3 of the reference cell.
\(\displaystyle l_{10}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{3}}\boldsymbol{v}\cdot(s_{0} \left(2 s_{0} - 1\right))\hat{\boldsymbol{t}}_{3}\)
where \(e_{3}\) is the 3rd edge;
\(\hat{\boldsymbol{t}}_{3}\) is the tangent to edge 3;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{3}\).
\(\displaystyle \boldsymbol{\phi}_{10} = \left(\begin{array}{c}\displaystyle \frac{y \left(600 x^{2} y^{2} - 540 x^{2} y + 60 x^{2} - 600 x y^{2} + 606 x y - 102 x + 140 y^{2} - 171 y + 43\right)}{4}\\\displaystyle \frac{x \left(- 600 x^{2} y^{2} + 600 x^{2} y - 100 x^{2} + 540 x y^{2} - 546 x y + 93 x + 60 y^{2} - 54 y + 7\right)}{4}\end{array}\right)\)
This DOF is associated with edge 3 of the reference cell.
where \(e_{3}\) is the 3rd edge;
\(\hat{\boldsymbol{t}}_{3}\) is the tangent to edge 3;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{3}\).
\(\displaystyle \boldsymbol{\phi}_{10} = \left(\begin{array}{c}\displaystyle \frac{y \left(600 x^{2} y^{2} - 540 x^{2} y + 60 x^{2} - 600 x y^{2} + 606 x y - 102 x + 140 y^{2} - 171 y + 43\right)}{4}\\\displaystyle \frac{x \left(- 600 x^{2} y^{2} + 600 x^{2} y - 100 x^{2} + 540 x y^{2} - 546 x y + 93 x + 60 y^{2} - 54 y + 7\right)}{4}\end{array}\right)\)
This DOF is associated with edge 3 of the reference cell.
\(\displaystyle l_{11}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{3}}\boldsymbol{v}\cdot(4 s_{0} \left(1 - s_{0}\right))\hat{\boldsymbol{t}}_{3}\)
where \(e_{3}\) is the 3rd edge;
\(\hat{\boldsymbol{t}}_{3}\) is the tangent to edge 3;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{3}\).
\(\displaystyle \boldsymbol{\phi}_{11} = \left(\begin{array}{c}\displaystyle \frac{y \left(- 300 x^{2} y^{2} + 270 x^{2} y - 30 x^{2} + 300 x y^{2} - 270 x y + 30 x - 10 y^{2} - 3 y + 7\right)}{4}\\\displaystyle \frac{25 x \left(12 x^{2} y^{2} - 12 x^{2} y + 2 x^{2} - 18 x y^{2} + 18 x y - 3 x + 6 y^{2} - 6 y + 1\right)}{4}\end{array}\right)\)
This DOF is associated with edge 3 of the reference cell.
where \(e_{3}\) is the 3rd edge;
\(\hat{\boldsymbol{t}}_{3}\) is the tangent to edge 3;
and \(s_{0},s_{1}\) is a parametrisation of \(e_{3}\).
\(\displaystyle \boldsymbol{\phi}_{11} = \left(\begin{array}{c}\displaystyle \frac{y \left(- 300 x^{2} y^{2} + 270 x^{2} y - 30 x^{2} + 300 x y^{2} - 270 x y + 30 x - 10 y^{2} - 3 y + 7\right)}{4}\\\displaystyle \frac{25 x \left(12 x^{2} y^{2} - 12 x^{2} y + 2 x^{2} - 18 x y^{2} + 18 x y - 3 x + 6 y^{2} - 6 y + 1\right)}{4}\end{array}\right)\)
This DOF is associated with edge 3 of the reference cell.
\(\displaystyle l_{12}:\mathbf{v}\mapsto\displaystyle\int_{R}\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\end{array}\right)\cdot\mathbf{v}\)
where \(R\) is the reference element.
\(\displaystyle \boldsymbol{\phi}_{12} = \left(\begin{array}{c}\displaystyle 6 y \left(150 x^{2} y^{2} - 255 x^{2} y + 105 x^{2} - 150 x y^{2} + 258 x y - 108 x + 35 y^{2} - 60 y + 25\right)\\\displaystyle 6 x \left(- 150 x^{2} y^{2} + 150 x^{2} y - 25 x^{2} + 315 x y^{2} - 318 x y + 54 x - 165 y^{2} + 168 y - 29\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
where \(R\) is the reference element.
\(\displaystyle \boldsymbol{\phi}_{12} = \left(\begin{array}{c}\displaystyle 6 y \left(150 x^{2} y^{2} - 255 x^{2} y + 105 x^{2} - 150 x y^{2} + 258 x y - 108 x + 35 y^{2} - 60 y + 25\right)\\\displaystyle 6 x \left(- 150 x^{2} y^{2} + 150 x^{2} y - 25 x^{2} + 315 x y^{2} - 318 x y + 54 x - 165 y^{2} + 168 y - 29\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{13}:\mathbf{v}\mapsto\displaystyle\int_{R}\left(\begin{array}{c}\displaystyle 2 s_{1}\\\displaystyle 0\end{array}\right)\cdot\mathbf{v}\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{13} = \left(\begin{array}{c}\displaystyle 15 y \left(- 60 x^{2} y^{2} + 90 x^{2} y - 30 x^{2} + 60 x y^{2} - 90 x y + 30 x - 14 y^{2} + 21 y - 7\right)\\\displaystyle 15 x \left(60 x^{2} y^{2} - 60 x^{2} y + 10 x^{2} - 126 x y^{2} + 126 x y - 21 x + 66 y^{2} - 66 y + 11\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{13} = \left(\begin{array}{c}\displaystyle 15 y \left(- 60 x^{2} y^{2} + 90 x^{2} y - 30 x^{2} + 60 x y^{2} - 90 x y + 30 x - 14 y^{2} + 21 y - 7\right)\\\displaystyle 15 x \left(60 x^{2} y^{2} - 60 x^{2} y + 10 x^{2} - 126 x y^{2} + 126 x y - 21 x + 66 y^{2} - 66 y + 11\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{14}:\mathbf{v}\mapsto\displaystyle\int_{R}\left(\begin{array}{c}\displaystyle 0\\\displaystyle -1\end{array}\right)\cdot\mathbf{v}\)
where \(R\) is the reference element.
\(\displaystyle \boldsymbol{\phi}_{14} = \left(\begin{array}{c}\displaystyle 6 y \left(150 x^{2} y^{2} - 315 x^{2} y + 165 x^{2} - 150 x y^{2} + 318 x y - 168 x + 25 y^{2} - 54 y + 29\right)\\\displaystyle 6 x \left(- 150 x^{2} y^{2} + 150 x^{2} y - 35 x^{2} + 255 x y^{2} - 258 x y + 60 x - 105 y^{2} + 108 y - 25\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
where \(R\) is the reference element.
\(\displaystyle \boldsymbol{\phi}_{14} = \left(\begin{array}{c}\displaystyle 6 y \left(150 x^{2} y^{2} - 315 x^{2} y + 165 x^{2} - 150 x y^{2} + 318 x y - 168 x + 25 y^{2} - 54 y + 29\right)\\\displaystyle 6 x \left(- 150 x^{2} y^{2} + 150 x^{2} y - 35 x^{2} + 255 x y^{2} - 258 x y + 60 x - 105 y^{2} + 108 y - 25\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
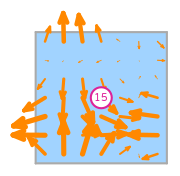
\(\displaystyle l_{15}:\mathbf{v}\mapsto\displaystyle\int_{R}\left(\begin{array}{c}\displaystyle s_{0}\\\displaystyle - s_{1}\end{array}\right)\cdot\mathbf{v}\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{15} = \left(\begin{array}{c}\displaystyle 36 y \left(- 150 x^{2} y^{2} + 255 x^{2} y - 105 x^{2} + 150 x y^{2} - 256 x y + 106 x - 25 y^{2} + 43 y - 18\right)\\\displaystyle 36 x \left(150 x^{2} y^{2} - 150 x^{2} y + 25 x^{2} - 255 x y^{2} + 256 x y - 43 x + 105 y^{2} - 106 y + 18\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{15} = \left(\begin{array}{c}\displaystyle 36 y \left(- 150 x^{2} y^{2} + 255 x^{2} y - 105 x^{2} + 150 x y^{2} - 256 x y + 106 x - 25 y^{2} + 43 y - 18\right)\\\displaystyle 36 x \left(150 x^{2} y^{2} - 150 x^{2} y + 25 x^{2} - 255 x y^{2} + 256 x y - 43 x + 105 y^{2} - 106 y + 18\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
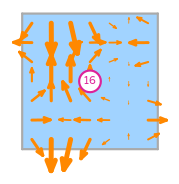
\(\displaystyle l_{16}:\mathbf{v}\mapsto\displaystyle\int_{R}\left(\begin{array}{c}\displaystyle 2 s_{0} s_{1}\\\displaystyle - s_{1}^{2}\end{array}\right)\cdot\mathbf{v}\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{16} = \left(\begin{array}{c}\displaystyle 450 y \left(12 x^{2} y^{2} - 18 x^{2} y + 6 x^{2} - 12 x y^{2} + 18 x y - 6 x + 2 y^{2} - 3 y + 1\right)\\\displaystyle 90 x \left(- 60 x^{2} y^{2} + 60 x^{2} y - 10 x^{2} + 102 x y^{2} - 102 x y + 17 x - 42 y^{2} + 42 y - 7\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{16} = \left(\begin{array}{c}\displaystyle 450 y \left(12 x^{2} y^{2} - 18 x^{2} y + 6 x^{2} - 12 x y^{2} + 18 x y - 6 x + 2 y^{2} - 3 y + 1\right)\\\displaystyle 90 x \left(- 60 x^{2} y^{2} + 60 x^{2} y - 10 x^{2} + 102 x y^{2} - 102 x y + 17 x - 42 y^{2} + 42 y - 7\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{17}:\mathbf{v}\mapsto\displaystyle\int_{R}\left(\begin{array}{c}\displaystyle 0\\\displaystyle - 2 s_{0}\end{array}\right)\cdot\mathbf{v}\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{17} = \left(\begin{array}{c}\displaystyle 15 y \left(- 60 x^{2} y^{2} + 126 x^{2} y - 66 x^{2} + 60 x y^{2} - 126 x y + 66 x - 10 y^{2} + 21 y - 11\right)\\\displaystyle 15 x \left(60 x^{2} y^{2} - 60 x^{2} y + 14 x^{2} - 90 x y^{2} + 90 x y - 21 x + 30 y^{2} - 30 y + 7\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{17} = \left(\begin{array}{c}\displaystyle 15 y \left(- 60 x^{2} y^{2} + 126 x^{2} y - 66 x^{2} + 60 x y^{2} - 126 x y + 66 x - 10 y^{2} + 21 y - 11\right)\\\displaystyle 15 x \left(60 x^{2} y^{2} - 60 x^{2} y + 14 x^{2} - 90 x y^{2} + 90 x y - 21 x + 30 y^{2} - 30 y + 7\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
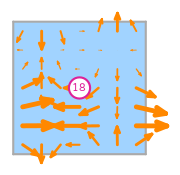
\(\displaystyle l_{18}:\mathbf{v}\mapsto\displaystyle\int_{R}\left(\begin{array}{c}\displaystyle s_{0}^{2}\\\displaystyle - 2 s_{0} s_{1}\end{array}\right)\cdot\mathbf{v}\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{18} = \left(\begin{array}{c}\displaystyle 90 y \left(60 x^{2} y^{2} - 102 x^{2} y + 42 x^{2} - 60 x y^{2} + 102 x y - 42 x + 10 y^{2} - 17 y + 7\right)\\\displaystyle 450 x \left(- 12 x^{2} y^{2} + 12 x^{2} y - 2 x^{2} + 18 x y^{2} - 18 x y + 3 x - 6 y^{2} + 6 y - 1\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{18} = \left(\begin{array}{c}\displaystyle 90 y \left(60 x^{2} y^{2} - 102 x^{2} y + 42 x^{2} - 60 x y^{2} + 102 x y - 42 x + 10 y^{2} - 17 y + 7\right)\\\displaystyle 450 x \left(- 12 x^{2} y^{2} + 12 x^{2} y - 2 x^{2} + 18 x y^{2} - 18 x y + 3 x - 6 y^{2} + 6 y - 1\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{19}:\mathbf{v}\mapsto\displaystyle\int_{R}\left(\begin{array}{c}\displaystyle 2 s_{0}^{2} s_{1}\\\displaystyle - 2 s_{0} s_{1}^{2}\end{array}\right)\cdot\mathbf{v}\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{19} = \left(\begin{array}{c}\displaystyle 450 y \left(- 12 x^{2} y^{2} + 18 x^{2} y - 6 x^{2} + 12 x y^{2} - 18 x y + 6 x - 2 y^{2} + 3 y - 1\right)\\\displaystyle 450 x \left(12 x^{2} y^{2} - 12 x^{2} y + 2 x^{2} - 18 x y^{2} + 18 x y - 3 x + 6 y^{2} - 6 y + 1\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{19} = \left(\begin{array}{c}\displaystyle 450 y \left(- 12 x^{2} y^{2} + 18 x^{2} y - 6 x^{2} + 12 x y^{2} - 18 x y + 6 x - 2 y^{2} + 3 y - 1\right)\\\displaystyle 450 x \left(12 x^{2} y^{2} - 12 x^{2} y + 2 x^{2} - 18 x y^{2} + 18 x y - 3 x + 6 y^{2} - 6 y + 1\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{20}:\mathbf{v}\mapsto\displaystyle\int_{R}\left(\begin{array}{c}\displaystyle s_{1} \left(- 2 s_{0} s_{1} + 2 s_{0} + s_{1} - 1\right)\\\displaystyle s_{0} \left(- 2 s_{0} s_{1} + s_{0} + 2 s_{1} - 1\right)\end{array}\right)\cdot\mathbf{v}\)
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{20} = \left(\begin{array}{c}\displaystyle 45 y \left(- 2 x y + 2 x + y - 1\right)\\\displaystyle 45 x \left(- 2 x y + x + 2 y - 1\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.
where \(R\) is the reference element;
and \(s_{0},s_{1}\) is a parametrisation of \(R\).
\(\displaystyle \boldsymbol{\phi}_{20} = \left(\begin{array}{c}\displaystyle 45 y \left(- 2 x y + 2 x + y - 1\right)\\\displaystyle 45 x \left(- 2 x y + x + 2 y - 1\right)\end{array}\right)\)
This DOF is associated with face 0 of the reference cell.