an encyclopedia of finite element definitions
Degree 3 Taylor on a triangle
◀ Back to Taylor definition page
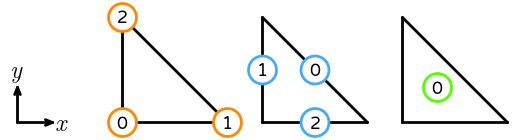
- \(R\) is the reference triangle. The following numbering of the sub-entities of the reference cell is used:
- \(\mathcal{V}\) is spanned by: \(1\), \(x\), \(x^{2}\), \(x^{3}\), \(y\), \(x y\), \(x^{2} y\), \(y^{2}\), \(x y^{2}\), \(y^{3}\)
- \(\mathcal{L}=\{l_0,...,l_{9}\}\)
- Functionals and basis functions:
\(\displaystyle l_{0}:v\mapsto\displaystyle\int_{R}v\)
where \(R\) is the reference element.
\(\displaystyle \phi_{0} = 2\)
This DOF is associated with face 0 of the reference cell.
where \(R\) is the reference element.
\(\displaystyle \phi_{0} = 2\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{1}:v\mapsto\frac{\partial}{\partial y}v(\tfrac{1}{3},\tfrac{1}{3})\)
\(\displaystyle \phi_{1} = y - \frac{1}{3}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle \phi_{1} = y - \frac{1}{3}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{2}:v\mapsto\frac{\partial^{2}}{\partial y^{2}}v(\tfrac{1}{3},\tfrac{1}{3})\)
\(\displaystyle \phi_{2} = \frac{y^{2}}{2} - \frac{y}{3} + \frac{1}{36}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle \phi_{2} = \frac{y^{2}}{2} - \frac{y}{3} + \frac{1}{36}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{3}:v\mapsto\frac{\partial^{3}}{\partial y^{3}}v(\tfrac{1}{3},\tfrac{1}{3})\)
\(\displaystyle \phi_{3} = \frac{y^{3}}{6} - \frac{y^{2}}{6} + \frac{y}{18} - \frac{1}{135}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle \phi_{3} = \frac{y^{3}}{6} - \frac{y^{2}}{6} + \frac{y}{18} - \frac{1}{135}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{4}:v\mapsto\frac{\partial}{\partial x}v(\tfrac{1}{3},\tfrac{1}{3})\)
\(\displaystyle \phi_{4} = x - \frac{1}{3}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle \phi_{4} = x - \frac{1}{3}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{5}:v\mapsto\frac{\partial^{2}}{\partial x\partial y}v(\tfrac{1}{3},\tfrac{1}{3})\)
\(\displaystyle \phi_{5} = x y - \frac{x}{3} - \frac{y}{3} + \frac{5}{36}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle \phi_{5} = x y - \frac{x}{3} - \frac{y}{3} + \frac{5}{36}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{6}:v\mapsto\frac{\partial^{3}}{\partial x\partial y^{2}}v(\tfrac{1}{3},\tfrac{1}{3})\)
\(\displaystyle \phi_{6} = \frac{x y^{2}}{2} - \frac{x y}{3} + \frac{x}{18} - \frac{y^{2}}{6} + \frac{y}{9} - \frac{1}{60}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle \phi_{6} = \frac{x y^{2}}{2} - \frac{x y}{3} + \frac{x}{18} - \frac{y^{2}}{6} + \frac{y}{9} - \frac{1}{60}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{7}:v\mapsto\frac{\partial^{2}}{\partial x^{2}}v(\tfrac{1}{3},\tfrac{1}{3})\)
\(\displaystyle \phi_{7} = \frac{x^{2}}{2} - \frac{x}{3} + \frac{1}{36}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle \phi_{7} = \frac{x^{2}}{2} - \frac{x}{3} + \frac{1}{36}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle l_{8}:v\mapsto\frac{\partial^{3}}{\partial x^{2}\partial y}v(\tfrac{1}{3},\tfrac{1}{3})\)
\(\displaystyle \phi_{8} = \frac{x^{2} y}{2} - \frac{x^{2}}{6} - \frac{x y}{3} + \frac{x}{9} + \frac{y}{18} - \frac{1}{60}\)
This DOF is associated with face 0 of the reference cell.
\(\displaystyle \phi_{8} = \frac{x^{2} y}{2} - \frac{x^{2}}{6} - \frac{x y}{3} + \frac{x}{9} + \frac{y}{18} - \frac{1}{60}\)
This DOF is associated with face 0 of the reference cell.