an encyclopedia of finite element definitions

Hellan–Herrmann–Johnson

Click here to read what the information on this page means.

Degrees	\(0\leqslant k\) where \(k\) is the Polynomial subdegree
Polynomial subdegree	\(k\)
Polynomial superdegree	\(k\)
Reference cells	triangle, tetrahedron
Polynomial set	\(\mathcal{Z}^{(2)}_{k}\) ↓ Show polynomial set definitions ↓↑ Hide polynomial set definitions ↑ \(\mathcal{Z}^{(2)}_k=\left\{\mathbf{M}\in\mathcal{P}_{k}^{d\times d}\middle\|\mathbf{M}^t=\mathbf{M}\right\}\) \(\mathcal{P}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle\|\sum_{i=1}^dp_i\leqslant k\right\}\)
DOFs	On each facet: integral moments of inner products of normal with a degree \(k\) Lagrange space On the interior of the reference cell (triangle): integrals against tensor products with symmetric matrices whose entries are in a degree \(k-1\) Lagrange space On the interior of the reference cell (tetrahedron): integrals against tensor products with symmetric matrices whose entries are in a degree \(k-1\) Lagrange space, and integrals against tensor products with the matrices \(\frac12(\boldsymbol{n}_1\boldsymbol{n}_2^{\text{t}}+\boldsymbol{n}_2\boldsymbol{n}_1^{\text{t}})\) and \(\frac12(\boldsymbol{n}_2\boldsymbol{n}_3^{\text{t}}+\boldsymbol{n}_3\boldsymbol{n}_2^{\text{t}})\) multiplied by degree \(k\) polynomials
Number of DOFs	triangle: \(3(k+1)(k+2)/2\) (A045943)
Mapping	double contravariant Piola
continuity	Inner products with normals to facets are continuous
Categories	Matrix-valued elements

Implementations

This element is implemented in Basix , Basix.UFL , FIAT , Symfem , and (legacy) UFL.↓ Show implementation detail ↓

↑ Hide implementation detail ↑

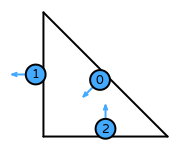
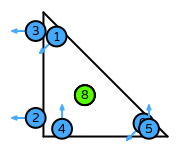
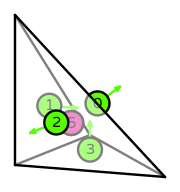
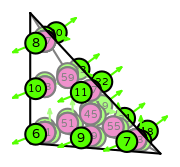
Basix	`basix.ElementFamily.HHJ` ↓ Show Basix examples ↓↑ Hide Basix examples ↑ Before running this example, you must install Basix: pip3 install git+https://github.com/FEniCS/basix This element can then be created with the following lines of Python: import basix # Create Hellan-Herrmann-Johnson degree 0 on a triangle element = basix.create_element(basix.ElementFamily.HHJ, basix.CellType.triangle, 0) # Create Hellan-Herrmann-Johnson degree 1 on a triangle element = basix.create_element(basix.ElementFamily.HHJ, basix.CellType.triangle, 1) # Create Hellan-Herrmann-Johnson degree 2 on a triangle element = basix.create_element(basix.ElementFamily.HHJ, basix.CellType.triangle, 2) # Create Hellan-Herrmann-Johnson degree 0 on a tetrahedron element = basix.create_element(basix.ElementFamily.HHJ, basix.CellType.tetrahedron, 0) # Create Hellan-Herrmann-Johnson degree 1 on a tetrahedron element = basix.create_element(basix.ElementFamily.HHJ, basix.CellType.tetrahedron, 1) # Create Hellan-Herrmann-Johnson degree 2 on a tetrahedron element = basix.create_element(basix.ElementFamily.HHJ, basix.CellType.tetrahedron, 2) This implementation is correct for all the examples below.
Basix.UFL	`basix.ElementFamily.HHJ` ↓ Show Basix.UFL examples ↓↑ Hide Basix.UFL examples ↑ Before running this example, you must install Basix.UFL: pip3 install git+https://github.com/FEniCS/basix fenics-ufl This element can then be created with the following lines of Python: import basix import basix.ufl # Create Hellan-Herrmann-Johnson degree 0 on a triangle element = basix.ufl.element(basix.ElementFamily.HHJ, basix.CellType.triangle, 0) # Create Hellan-Herrmann-Johnson degree 1 on a triangle element = basix.ufl.element(basix.ElementFamily.HHJ, basix.CellType.triangle, 1) # Create Hellan-Herrmann-Johnson degree 2 on a triangle element = basix.ufl.element(basix.ElementFamily.HHJ, basix.CellType.triangle, 2) # Create Hellan-Herrmann-Johnson degree 0 on a tetrahedron element = basix.ufl.element(basix.ElementFamily.HHJ, basix.CellType.tetrahedron, 0) # Create Hellan-Herrmann-Johnson degree 1 on a tetrahedron element = basix.ufl.element(basix.ElementFamily.HHJ, basix.CellType.tetrahedron, 1) # Create Hellan-Herrmann-Johnson degree 2 on a tetrahedron element = basix.ufl.element(basix.ElementFamily.HHJ, basix.CellType.tetrahedron, 2) This implementation is correct for all the examples below.
FIAT	`FIAT.HellanHerrmannJohnson` ↓ Show FIAT examples ↓↑ Hide FIAT examples ↑ Before running this example, you must install FIAT: pip3 install git+https://github.com/firedrakeproject/fiat.git This element can then be created with the following lines of Python: import FIAT # Create Hellan-Herrmann-Johnson degree 0 element = FIAT.HellanHerrmannJohnson(FIAT.ufc_cell("triangle"), 0) # Create Hellan-Herrmann-Johnson degree 1 element = FIAT.HellanHerrmannJohnson(FIAT.ufc_cell("triangle"), 1) # Create Hellan-Herrmann-Johnson degree 2 element = FIAT.HellanHerrmannJohnson(FIAT.ufc_cell("triangle"), 2) # Create Hellan-Herrmann-Johnson degree 0 element = FIAT.HellanHerrmannJohnson(FIAT.ufc_cell("tetrahedron"), 0) # Create Hellan-Herrmann-Johnson degree 1 element = FIAT.HellanHerrmannJohnson(FIAT.ufc_cell("tetrahedron"), 1) # Create Hellan-Herrmann-Johnson degree 2 element = FIAT.HellanHerrmannJohnson(FIAT.ufc_cell("tetrahedron"), 2) This implementation is correct for all the examples below.
Symfem	`"HHJ"` ↓ Show Symfem examples ↓↑ Hide Symfem examples ↑ Before running this example, you must install Symfem: pip3 install symfem This element can then be created with the following lines of Python: import symfem # Create Hellan-Herrmann-Johnson degree 0 on a triangle element = symfem.create_element("triangle", "HHJ", 0) # Create Hellan-Herrmann-Johnson degree 1 on a triangle element = symfem.create_element("triangle", "HHJ", 1) # Create Hellan-Herrmann-Johnson degree 2 on a triangle element = symfem.create_element("triangle", "HHJ", 2) # Create Hellan-Herrmann-Johnson degree 0 on a tetrahedron element = symfem.create_element("tetrahedron", "HHJ", 0) # Create Hellan-Herrmann-Johnson degree 1 on a tetrahedron element = symfem.create_element("tetrahedron", "HHJ", 1) # Create Hellan-Herrmann-Johnson degree 2 on a tetrahedron element = symfem.create_element("tetrahedron", "HHJ", 2) This implementation is used to compute the examples below and verify other implementations.
(legacy) UFL	`"HHJ"` ↓ Show (legacy) UFL examples ↓↑ Hide (legacy) UFL examples ↑ Before running this example, you must install (legacy) UFL: pip3 install setuptools pip3 install fenics-ufl-legacy This element can then be created with the following lines of Python: import ufl_legacy # Create Hellan-Herrmann-Johnson degree 0 on a triangle element = ufl_legacy.FiniteElement("HHJ", "triangle", 0) # Create Hellan-Herrmann-Johnson degree 1 on a triangle element = ufl_legacy.FiniteElement("HHJ", "triangle", 1) # Create Hellan-Herrmann-Johnson degree 2 on a triangle element = ufl_legacy.FiniteElement("HHJ", "triangle", 2)

Examples

triangle degree 0	(click to view basis functions)
triangle degree 1	(click to view basis functions)
triangle degree 2	(click to view basis functions)
tetrahedron degree 0	(click to view basis functions)
tetrahedron degree 1	(click to view basis functions)
tetrahedron degree 2	(click to view basis functions)

References

Arnold, Douglas N. and Walker, Shawn W. The Hellan–Herrmann–Johnson method with curved elements, SIAM Journal on Numberical Analysis 58(5), 2829–2855, 2020. [DOI: 10.1137/19M1288723] [BibTeX]
Pechstein, Astrid S. and Schöberl, Joachim. An analysis of the TDNNS method using natural norms, Numerische Mathematik 139, 92–120, 2018. [DOI: 10.1007/s00211-017-0933-3] [BibTeX]

DefElement stats

Element added	04 March 2025
Element last updated	04 June 2025