an encyclopedia of finite element definitions
Degree 2 Nédélec (first kind) on a prism
◀ Back to Nédélec (first kind) definition page
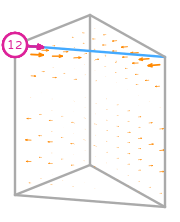
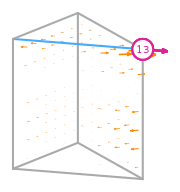
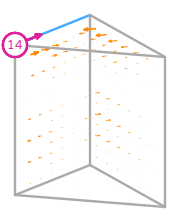
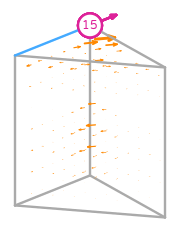
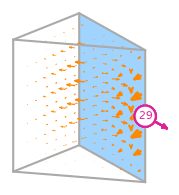
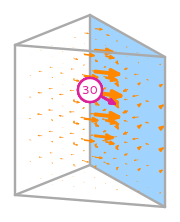
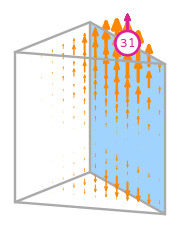
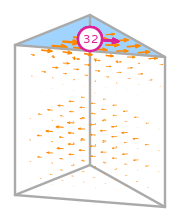
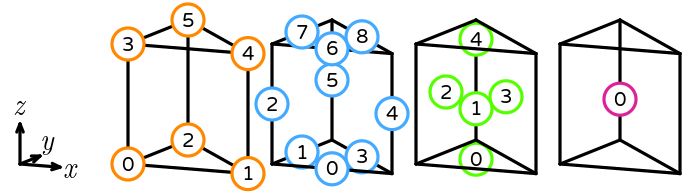
- \(R\) is the reference prism. The following numbering of the subentities of the reference is used:
- \(\mathcal{V}\) is spanned by: \(\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle z\\\displaystyle 0\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle z^{2}\\\displaystyle 0\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle z\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle z^{2}\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle x\\\displaystyle 0\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle x z\\\displaystyle 0\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle x z^{2}\\\displaystyle 0\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle x\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle x z\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle x z^{2}\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle y\\\displaystyle 0\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle y z\\\displaystyle 0\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle y z^{2}\\\displaystyle 0\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle y\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle y z\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle y z^{2}\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle x y\\\displaystyle - x^{2}\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle x y z\\\displaystyle - x^{2} z\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle x y z^{2}\\\displaystyle - x^{2} z^{2}\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle y^{2}\\\displaystyle - x y\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle y^{2} z\\\displaystyle - x y z\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle y^{2} z^{2}\\\displaystyle - x y z^{2}\\\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 1\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle z\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x z\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x^{2}\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x^{2} z\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle y\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle y z\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x y\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x y z\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle y^{2}\end{array}\right)\), \(\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle y^{2} z\end{array}\right)\)
- \(\mathcal{L}=\{l_0,...,l_{35}\}\)
- Functionals and basis functions:
\(\displaystyle l_{0}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{0}}\boldsymbol{v}\cdot(1 - s_{0})\hat{\boldsymbol{t}}_{0}\)
where \(e_{0}\) is the 0th edge;
\(\hat{\boldsymbol{t}}_{0}\) is the tangent to edge 0;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \boldsymbol{\phi}_{0} = \left(\begin{array}{c}\displaystyle 24 x y z^{2} - 32 x y z + 8 x y - 18 x z^{2} + 24 x z - 6 x + 24 y^{2} z^{2} - 32 y^{2} z + 8 y^{2} - 36 y z^{2} + 48 y z - 12 y + 12 z^{2} - 16 z + 4\\\displaystyle 2 x \left(- 12 x z^{2} + 16 x z - 4 x - 12 y z^{2} + 16 y z - 4 y + 9 z^{2} - 12 z + 3\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
where \(e_{0}\) is the 0th edge;
\(\hat{\boldsymbol{t}}_{0}\) is the tangent to edge 0;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \boldsymbol{\phi}_{0} = \left(\begin{array}{c}\displaystyle 24 x y z^{2} - 32 x y z + 8 x y - 18 x z^{2} + 24 x z - 6 x + 24 y^{2} z^{2} - 32 y^{2} z + 8 y^{2} - 36 y z^{2} + 48 y z - 12 y + 12 z^{2} - 16 z + 4\\\displaystyle 2 x \left(- 12 x z^{2} + 16 x z - 4 x - 12 y z^{2} + 16 y z - 4 y + 9 z^{2} - 12 z + 3\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle l_{1}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{0}}\boldsymbol{v}\cdot(s_{0})\hat{\boldsymbol{t}}_{0}\)
where \(e_{0}\) is the 0th edge;
\(\hat{\boldsymbol{t}}_{0}\) is the tangent to edge 0;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{0}\).
\(\displaystyle \boldsymbol{\phi}_{1} = \left(\begin{array}{c}\displaystyle - 24 x y z^{2} + 32 x y z - 8 x y + 18 x z^{2} - 24 x z + 6 x + 6 y z^{2} - 8 y z + 2 y - 6 z^{2} + 8 z - 2\\\displaystyle 4 x \left(6 x z^{2} - 8 x z + 2 x - 3 z^{2} + 4 z - 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 0 of the reference element.
where \(e_{0}\) is the 0th edge;
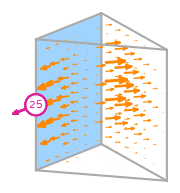
\(\hat{\boldsymbol{t}}_{0}\) is the tangent to edge 0;
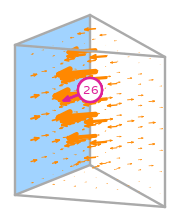
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{0}\).
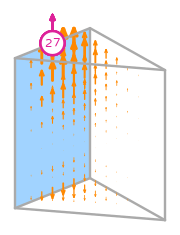
\(\displaystyle \boldsymbol{\phi}_{1} = \left(\begin{array}{c}\displaystyle - 24 x y z^{2} + 32 x y z - 8 x y + 18 x z^{2} - 24 x z + 6 x + 6 y z^{2} - 8 y z + 2 y - 6 z^{2} + 8 z - 2\\\displaystyle 4 x \left(6 x z^{2} - 8 x z + 2 x - 3 z^{2} + 4 z - 1\right)\\\displaystyle 0\end{array}\right)\)
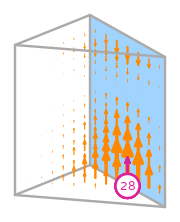
This DOF is associated with edge 0 of the reference element.
\(\displaystyle l_{2}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{1}}\boldsymbol{v}\cdot(1 - s_{0})\hat{\boldsymbol{t}}_{1}\)
where \(e_{1}\) is the 1st edge;
\(\hat{\boldsymbol{t}}_{1}\) is the tangent to edge 1;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \boldsymbol{\phi}_{2} = \left(\begin{array}{c}\displaystyle 2 y \left(- 12 x z^{2} + 16 x z - 4 x - 12 y z^{2} + 16 y z - 4 y + 9 z^{2} - 12 z + 3\right)\\\displaystyle 24 x^{2} z^{2} - 32 x^{2} z + 8 x^{2} + 24 x y z^{2} - 32 x y z + 8 x y - 36 x z^{2} + 48 x z - 12 x - 18 y z^{2} + 24 y z - 6 y + 12 z^{2} - 16 z + 4\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
where \(e_{1}\) is the 1st edge;
\(\hat{\boldsymbol{t}}_{1}\) is the tangent to edge 1;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \boldsymbol{\phi}_{2} = \left(\begin{array}{c}\displaystyle 2 y \left(- 12 x z^{2} + 16 x z - 4 x - 12 y z^{2} + 16 y z - 4 y + 9 z^{2} - 12 z + 3\right)\\\displaystyle 24 x^{2} z^{2} - 32 x^{2} z + 8 x^{2} + 24 x y z^{2} - 32 x y z + 8 x y - 36 x z^{2} + 48 x z - 12 x - 18 y z^{2} + 24 y z - 6 y + 12 z^{2} - 16 z + 4\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle l_{3}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{1}}\boldsymbol{v}\cdot(s_{0})\hat{\boldsymbol{t}}_{1}\)
where \(e_{1}\) is the 1st edge;
\(\hat{\boldsymbol{t}}_{1}\) is the tangent to edge 1;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \boldsymbol{\phi}_{3} = \left(\begin{array}{c}\displaystyle 4 y \left(6 y z^{2} - 8 y z + 2 y - 3 z^{2} + 4 z - 1\right)\\\displaystyle - 24 x y z^{2} + 32 x y z - 8 x y + 6 x z^{2} - 8 x z + 2 x + 18 y z^{2} - 24 y z + 6 y - 6 z^{2} + 8 z - 2\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
where \(e_{1}\) is the 1st edge;
\(\hat{\boldsymbol{t}}_{1}\) is the tangent to edge 1;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{1}\).
\(\displaystyle \boldsymbol{\phi}_{3} = \left(\begin{array}{c}\displaystyle 4 y \left(6 y z^{2} - 8 y z + 2 y - 3 z^{2} + 4 z - 1\right)\\\displaystyle - 24 x y z^{2} + 32 x y z - 8 x y + 6 x z^{2} - 8 x z + 2 x + 18 y z^{2} - 24 y z + 6 y - 6 z^{2} + 8 z - 2\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle l_{4}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{2}}\boldsymbol{v}\cdot(1 - s_{0})\hat{\boldsymbol{t}}_{2}\)
where \(e_{2}\) is the 2nd edge;
\(\hat{\boldsymbol{t}}_{2}\) is the tangent to edge 2;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \boldsymbol{\phi}_{4} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle - 18 x^{2} z + 12 x^{2} - 36 x y z + 24 x y + 24 x z - 16 x - 18 y^{2} z + 12 y^{2} + 24 y z - 16 y - 6 z + 4\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
where \(e_{2}\) is the 2nd edge;
\(\hat{\boldsymbol{t}}_{2}\) is the tangent to edge 2;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \boldsymbol{\phi}_{4} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle - 18 x^{2} z + 12 x^{2} - 36 x y z + 24 x y + 24 x z - 16 x - 18 y^{2} z + 12 y^{2} + 24 y z - 16 y - 6 z + 4\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle l_{5}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{2}}\boldsymbol{v}\cdot(s_{0})\hat{\boldsymbol{t}}_{2}\)
where \(e_{2}\) is the 2nd edge;
\(\hat{\boldsymbol{t}}_{2}\) is the tangent to edge 2;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \boldsymbol{\phi}_{5} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 18 x^{2} z - 6 x^{2} + 36 x y z - 12 x y - 24 x z + 8 x + 18 y^{2} z - 6 y^{2} - 24 y z + 8 y + 6 z - 2\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
where \(e_{2}\) is the 2nd edge;
\(\hat{\boldsymbol{t}}_{2}\) is the tangent to edge 2;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{2}\).
\(\displaystyle \boldsymbol{\phi}_{5} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 18 x^{2} z - 6 x^{2} + 36 x y z - 12 x y - 24 x z + 8 x + 18 y^{2} z - 6 y^{2} - 24 y z + 8 y + 6 z - 2\end{array}\right)\)
This DOF is associated with edge 2 of the reference element.
\(\displaystyle l_{6}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{3}}\boldsymbol{v}\cdot(1 - s_{0})\hat{\boldsymbol{t}}_{3}\)
where \(e_{3}\) is the 3rd edge;
\(\hat{\boldsymbol{t}}_{3}\) is the tangent to edge 3;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{3}\).
\(\displaystyle \boldsymbol{\phi}_{6} = \left(\begin{array}{c}\displaystyle 2 y \left(- 12 x z^{2} + 16 x z - 4 x + 3 z^{2} - 4 z + 1\right)\\\displaystyle 4 x \left(6 x z^{2} - 8 x z + 2 x - 3 z^{2} + 4 z - 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 3 of the reference element.
where \(e_{3}\) is the 3rd edge;
\(\hat{\boldsymbol{t}}_{3}\) is the tangent to edge 3;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{3}\).
\(\displaystyle \boldsymbol{\phi}_{6} = \left(\begin{array}{c}\displaystyle 2 y \left(- 12 x z^{2} + 16 x z - 4 x + 3 z^{2} - 4 z + 1\right)\\\displaystyle 4 x \left(6 x z^{2} - 8 x z + 2 x - 3 z^{2} + 4 z - 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 3 of the reference element.
\(\displaystyle l_{7}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{3}}\boldsymbol{v}\cdot(s_{0})\hat{\boldsymbol{t}}_{3}\)
where \(e_{3}\) is the 3rd edge;
\(\hat{\boldsymbol{t}}_{3}\) is the tangent to edge 3;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{3}\).
\(\displaystyle \boldsymbol{\phi}_{7} = \left(\begin{array}{c}\displaystyle 4 y \left(- 6 y z^{2} + 8 y z - 2 y + 3 z^{2} - 4 z + 1\right)\\\displaystyle 2 x \left(12 y z^{2} - 16 y z + 4 y - 3 z^{2} + 4 z - 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 3 of the reference element.
where \(e_{3}\) is the 3rd edge;
\(\hat{\boldsymbol{t}}_{3}\) is the tangent to edge 3;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{3}\).
\(\displaystyle \boldsymbol{\phi}_{7} = \left(\begin{array}{c}\displaystyle 4 y \left(- 6 y z^{2} + 8 y z - 2 y + 3 z^{2} - 4 z + 1\right)\\\displaystyle 2 x \left(12 y z^{2} - 16 y z + 4 y - 3 z^{2} + 4 z - 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 3 of the reference element.
\(\displaystyle l_{8}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{4}}\boldsymbol{v}\cdot(1 - s_{0})\hat{\boldsymbol{t}}_{4}\)
where \(e_{4}\) is the 4th edge;
\(\hat{\boldsymbol{t}}_{4}\) is the tangent to edge 4;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{4}\).
\(\displaystyle \boldsymbol{\phi}_{8} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2 x \left(- 9 x z + 6 x + 6 z - 4\right)\end{array}\right)\)
This DOF is associated with edge 4 of the reference element.
where \(e_{4}\) is the 4th edge;
\(\hat{\boldsymbol{t}}_{4}\) is the tangent to edge 4;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{4}\).
\(\displaystyle \boldsymbol{\phi}_{8} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2 x \left(- 9 x z + 6 x + 6 z - 4\right)\end{array}\right)\)
This DOF is associated with edge 4 of the reference element.
\(\displaystyle l_{9}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{4}}\boldsymbol{v}\cdot(s_{0})\hat{\boldsymbol{t}}_{4}\)
where \(e_{4}\) is the 4th edge;
\(\hat{\boldsymbol{t}}_{4}\) is the tangent to edge 4;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{4}\).
\(\displaystyle \boldsymbol{\phi}_{9} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2 x \left(9 x z - 3 x - 6 z + 2\right)\end{array}\right)\)
This DOF is associated with edge 4 of the reference element.
where \(e_{4}\) is the 4th edge;
\(\hat{\boldsymbol{t}}_{4}\) is the tangent to edge 4;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{4}\).
\(\displaystyle \boldsymbol{\phi}_{9} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2 x \left(9 x z - 3 x - 6 z + 2\right)\end{array}\right)\)
This DOF is associated with edge 4 of the reference element.
\(\displaystyle l_{10}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{5}}\boldsymbol{v}\cdot(1 - s_{0})\hat{\boldsymbol{t}}_{5}\)
where \(e_{5}\) is the 5th edge;
\(\hat{\boldsymbol{t}}_{5}\) is the tangent to edge 5;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{5}\).
\(\displaystyle \boldsymbol{\phi}_{10} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2 y \left(- 9 y z + 6 y + 6 z - 4\right)\end{array}\right)\)
This DOF is associated with edge 5 of the reference element.
where \(e_{5}\) is the 5th edge;
\(\hat{\boldsymbol{t}}_{5}\) is the tangent to edge 5;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{5}\).
\(\displaystyle \boldsymbol{\phi}_{10} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2 y \left(- 9 y z + 6 y + 6 z - 4\right)\end{array}\right)\)
This DOF is associated with edge 5 of the reference element.
\(\displaystyle l_{11}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{5}}\boldsymbol{v}\cdot(s_{0})\hat{\boldsymbol{t}}_{5}\)
where \(e_{5}\) is the 5th edge;
\(\hat{\boldsymbol{t}}_{5}\) is the tangent to edge 5;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{5}\).
\(\displaystyle \boldsymbol{\phi}_{11} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2 y \left(9 y z - 3 y - 6 z + 2\right)\end{array}\right)\)
This DOF is associated with edge 5 of the reference element.
where \(e_{5}\) is the 5th edge;
\(\hat{\boldsymbol{t}}_{5}\) is the tangent to edge 5;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{5}\).
\(\displaystyle \boldsymbol{\phi}_{11} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2 y \left(9 y z - 3 y - 6 z + 2\right)\end{array}\right)\)
This DOF is associated with edge 5 of the reference element.
\(\displaystyle l_{12}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{6}}\boldsymbol{v}\cdot(1 - s_{0})\hat{\boldsymbol{t}}_{6}\)
where \(e_{6}\) is the 6th edge;
\(\hat{\boldsymbol{t}}_{6}\) is the tangent to edge 6;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{6}\).
\(\displaystyle \boldsymbol{\phi}_{12} = \left(\begin{array}{c}\displaystyle 2 z \left(12 x y z - 8 x y - 9 x z + 6 x + 12 y^{2} z - 8 y^{2} - 18 y z + 12 y + 6 z - 4\right)\\\displaystyle 2 x z \left(- 12 x z + 8 x - 12 y z + 8 y + 9 z - 6\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 6 of the reference element.
where \(e_{6}\) is the 6th edge;
\(\hat{\boldsymbol{t}}_{6}\) is the tangent to edge 6;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{6}\).
\(\displaystyle \boldsymbol{\phi}_{12} = \left(\begin{array}{c}\displaystyle 2 z \left(12 x y z - 8 x y - 9 x z + 6 x + 12 y^{2} z - 8 y^{2} - 18 y z + 12 y + 6 z - 4\right)\\\displaystyle 2 x z \left(- 12 x z + 8 x - 12 y z + 8 y + 9 z - 6\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 6 of the reference element.
\(\displaystyle l_{13}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{6}}\boldsymbol{v}\cdot(s_{0})\hat{\boldsymbol{t}}_{6}\)
where \(e_{6}\) is the 6th edge;
\(\hat{\boldsymbol{t}}_{6}\) is the tangent to edge 6;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{6}\).
\(\displaystyle \boldsymbol{\phi}_{13} = \left(\begin{array}{c}\displaystyle 2 z \left(- 12 x y z + 8 x y + 9 x z - 6 x + 3 y z - 2 y - 3 z + 2\right)\\\displaystyle 4 x z \left(6 x z - 4 x - 3 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 6 of the reference element.
where \(e_{6}\) is the 6th edge;
\(\hat{\boldsymbol{t}}_{6}\) is the tangent to edge 6;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{6}\).
\(\displaystyle \boldsymbol{\phi}_{13} = \left(\begin{array}{c}\displaystyle 2 z \left(- 12 x y z + 8 x y + 9 x z - 6 x + 3 y z - 2 y - 3 z + 2\right)\\\displaystyle 4 x z \left(6 x z - 4 x - 3 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 6 of the reference element.
\(\displaystyle l_{14}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{7}}\boldsymbol{v}\cdot(1 - s_{0})\hat{\boldsymbol{t}}_{7}\)
where \(e_{7}\) is the 7th edge;
\(\hat{\boldsymbol{t}}_{7}\) is the tangent to edge 7;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{7}\).
\(\displaystyle \boldsymbol{\phi}_{14} = \left(\begin{array}{c}\displaystyle 2 y z \left(- 12 x z + 8 x - 12 y z + 8 y + 9 z - 6\right)\\\displaystyle 2 z \left(12 x^{2} z - 8 x^{2} + 12 x y z - 8 x y - 18 x z + 12 x - 9 y z + 6 y + 6 z - 4\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 7 of the reference element.
where \(e_{7}\) is the 7th edge;
\(\hat{\boldsymbol{t}}_{7}\) is the tangent to edge 7;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{7}\).
\(\displaystyle \boldsymbol{\phi}_{14} = \left(\begin{array}{c}\displaystyle 2 y z \left(- 12 x z + 8 x - 12 y z + 8 y + 9 z - 6\right)\\\displaystyle 2 z \left(12 x^{2} z - 8 x^{2} + 12 x y z - 8 x y - 18 x z + 12 x - 9 y z + 6 y + 6 z - 4\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 7 of the reference element.
\(\displaystyle l_{15}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{7}}\boldsymbol{v}\cdot(s_{0})\hat{\boldsymbol{t}}_{7}\)
where \(e_{7}\) is the 7th edge;
\(\hat{\boldsymbol{t}}_{7}\) is the tangent to edge 7;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{7}\).
\(\displaystyle \boldsymbol{\phi}_{15} = \left(\begin{array}{c}\displaystyle 4 y z \left(6 y z - 4 y - 3 z + 2\right)\\\displaystyle 2 z \left(- 12 x y z + 8 x y + 3 x z - 2 x + 9 y z - 6 y - 3 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 7 of the reference element.
where \(e_{7}\) is the 7th edge;
\(\hat{\boldsymbol{t}}_{7}\) is the tangent to edge 7;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{7}\).
\(\displaystyle \boldsymbol{\phi}_{15} = \left(\begin{array}{c}\displaystyle 4 y z \left(6 y z - 4 y - 3 z + 2\right)\\\displaystyle 2 z \left(- 12 x y z + 8 x y + 3 x z - 2 x + 9 y z - 6 y - 3 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 7 of the reference element.
\(\displaystyle l_{16}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{8}}\boldsymbol{v}\cdot(1 - s_{0})\hat{\boldsymbol{t}}_{8}\)
where \(e_{8}\) is the 8th edge;
\(\hat{\boldsymbol{t}}_{8}\) is the tangent to edge 8;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{8}\).
\(\displaystyle \boldsymbol{\phi}_{16} = \left(\begin{array}{c}\displaystyle 2 y z \left(- 12 x z + 8 x + 3 z - 2\right)\\\displaystyle 4 x z \left(6 x z - 4 x - 3 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 8 of the reference element.
where \(e_{8}\) is the 8th edge;
\(\hat{\boldsymbol{t}}_{8}\) is the tangent to edge 8;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{8}\).
\(\displaystyle \boldsymbol{\phi}_{16} = \left(\begin{array}{c}\displaystyle 2 y z \left(- 12 x z + 8 x + 3 z - 2\right)\\\displaystyle 4 x z \left(6 x z - 4 x - 3 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 8 of the reference element.
\(\displaystyle l_{17}:\boldsymbol{v}\mapsto\displaystyle\int_{e_{8}}\boldsymbol{v}\cdot(s_{0})\hat{\boldsymbol{t}}_{8}\)
where \(e_{8}\) is the 8th edge;
\(\hat{\boldsymbol{t}}_{8}\) is the tangent to edge 8;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{8}\).
\(\displaystyle \boldsymbol{\phi}_{17} = \left(\begin{array}{c}\displaystyle 4 y z \left(- 6 y z + 4 y + 3 z - 2\right)\\\displaystyle 2 x z \left(12 y z - 8 y - 3 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 8 of the reference element.
where \(e_{8}\) is the 8th edge;
\(\hat{\boldsymbol{t}}_{8}\) is the tangent to edge 8;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(e_{8}\).
\(\displaystyle \boldsymbol{\phi}_{17} = \left(\begin{array}{c}\displaystyle 4 y z \left(- 6 y z + 4 y + 3 z - 2\right)\\\displaystyle 2 x z \left(12 y z - 8 y - 3 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with edge 8 of the reference element.
\(\displaystyle l_{18}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{0}}\boldsymbol{v}\cdot\left(\begin{array}{c}1\\0\\0\end{array}\right)\)
where \(f_{0}\) is the 0th face.
\(\displaystyle \boldsymbol{\phi}_{18} = \left(\begin{array}{c}\displaystyle 8 y \left(- 3 x z^{2} + 4 x z - x - 6 y z^{2} + 8 y z - 2 y + 6 z^{2} - 8 z + 2\right)\\\displaystyle 8 x \left(3 x z^{2} - 4 x z + x + 6 y z^{2} - 8 y z + 2 y - 3 z^{2} + 4 z - 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(f_{0}\) is the 0th face.
\(\displaystyle \boldsymbol{\phi}_{18} = \left(\begin{array}{c}\displaystyle 8 y \left(- 3 x z^{2} + 4 x z - x - 6 y z^{2} + 8 y z - 2 y + 6 z^{2} - 8 z + 2\right)\\\displaystyle 8 x \left(3 x z^{2} - 4 x z + x + 6 y z^{2} - 8 y z + 2 y - 3 z^{2} + 4 z - 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{19}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{0}}\boldsymbol{v}\cdot\left(\begin{array}{c}0\\1\\0\end{array}\right)\)
where \(f_{0}\) is the 0th face.
\(\displaystyle \boldsymbol{\phi}_{19} = \left(\begin{array}{c}\displaystyle 8 y \left(6 x z^{2} - 8 x z + 2 x + 3 y z^{2} - 4 y z + y - 3 z^{2} + 4 z - 1\right)\\\displaystyle 8 x \left(- 6 x z^{2} + 8 x z - 2 x - 3 y z^{2} + 4 y z - y + 6 z^{2} - 8 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(f_{0}\) is the 0th face.
\(\displaystyle \boldsymbol{\phi}_{19} = \left(\begin{array}{c}\displaystyle 8 y \left(6 x z^{2} - 8 x z + 2 x + 3 y z^{2} - 4 y z + y - 3 z^{2} + 4 z - 1\right)\\\displaystyle 8 x \left(- 6 x z^{2} + 8 x z - 2 x - 3 y z^{2} + 4 y z - y + 6 z^{2} - 8 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
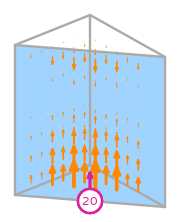
\(\displaystyle l_{20}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{1}}\boldsymbol{v}\cdot\left(\begin{array}{c}0\\0\\1 - s_{1}\end{array}\right)\)
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \boldsymbol{\phi}_{20} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 12 x \left(3 x z - 2 x + 3 y z - 2 y - 3 z + 2\right)\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \boldsymbol{\phi}_{20} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 12 x \left(3 x z - 2 x + 3 y z - 2 y - 3 z + 2\right)\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
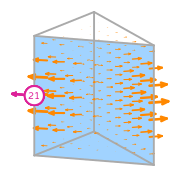
\(\displaystyle l_{21}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{1}}\boldsymbol{v}\cdot\left(\begin{array}{c}s_{0} - 1\\0\\0\end{array}\right)\)
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \boldsymbol{\phi}_{21} = \left(\begin{array}{c}\displaystyle 12 z \left(4 x y z - 4 x y - 3 x z + 3 x + 4 y^{2} z - 4 y^{2} - 6 y z + 6 y + 2 z - 2\right)\\\displaystyle 12 x z \left(- 4 x z + 4 x - 4 y z + 4 y + 3 z - 3\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \boldsymbol{\phi}_{21} = \left(\begin{array}{c}\displaystyle 12 z \left(4 x y z - 4 x y - 3 x z + 3 x + 4 y^{2} z - 4 y^{2} - 6 y z + 6 y + 2 z - 2\right)\\\displaystyle 12 x z \left(- 4 x z + 4 x - 4 y z + 4 y + 3 z - 3\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
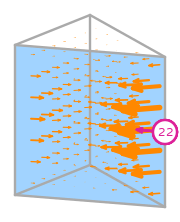
\(\displaystyle l_{22}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{1}}\boldsymbol{v}\cdot\left(\begin{array}{c}- s_{0}\\0\\0\end{array}\right)\)
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \boldsymbol{\phi}_{22} = \left(\begin{array}{c}\displaystyle 12 z \left(- 4 x y z + 4 x y + 3 x z - 3 x + y z - y - z + 1\right)\\\displaystyle 24 x z \left(2 x z - 2 x - z + 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \boldsymbol{\phi}_{22} = \left(\begin{array}{c}\displaystyle 12 z \left(- 4 x y z + 4 x y + 3 x z - 3 x + y z - y - z + 1\right)\\\displaystyle 24 x z \left(2 x z - 2 x - z + 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
\(\displaystyle l_{23}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{1}}\boldsymbol{v}\cdot\left(\begin{array}{c}0\\0\\s_{1}\end{array}\right)\)
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \boldsymbol{\phi}_{23} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 12 x \left(- 3 x z + x - 3 y z + y + 3 z - 1\right)\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \boldsymbol{\phi}_{23} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 12 x \left(- 3 x z + x - 3 y z + y + 3 z - 1\right)\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
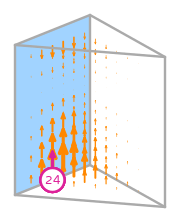
\(\displaystyle l_{24}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{2}}\boldsymbol{v}\cdot\left(\begin{array}{c}0\\0\\1 - s_{1}\end{array}\right)\)
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \boldsymbol{\phi}_{24} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 12 y \left(3 x z - 2 x + 3 y z - 2 y - 3 z + 2\right)\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \boldsymbol{\phi}_{24} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 12 y \left(3 x z - 2 x + 3 y z - 2 y - 3 z + 2\right)\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
\(\displaystyle l_{25}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{2}}\boldsymbol{v}\cdot\left(\begin{array}{c}0\\s_{0} - 1\\0\end{array}\right)\)
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \boldsymbol{\phi}_{25} = \left(\begin{array}{c}\displaystyle 12 y z \left(- 4 x z + 4 x - 4 y z + 4 y + 3 z - 3\right)\\\displaystyle 12 z \left(4 x^{2} z - 4 x^{2} + 4 x y z - 4 x y - 6 x z + 6 x - 3 y z + 3 y + 2 z - 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \boldsymbol{\phi}_{25} = \left(\begin{array}{c}\displaystyle 12 y z \left(- 4 x z + 4 x - 4 y z + 4 y + 3 z - 3\right)\\\displaystyle 12 z \left(4 x^{2} z - 4 x^{2} + 4 x y z - 4 x y - 6 x z + 6 x - 3 y z + 3 y + 2 z - 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
\(\displaystyle l_{26}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{2}}\boldsymbol{v}\cdot\left(\begin{array}{c}0\\- s_{0}\\0\end{array}\right)\)
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \boldsymbol{\phi}_{26} = \left(\begin{array}{c}\displaystyle 24 y z \left(2 y z - 2 y - z + 1\right)\\\displaystyle 12 z \left(- 4 x y z + 4 x y + x z - x + 3 y z - 3 y - z + 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \boldsymbol{\phi}_{26} = \left(\begin{array}{c}\displaystyle 24 y z \left(2 y z - 2 y - z + 1\right)\\\displaystyle 12 z \left(- 4 x y z + 4 x y + x z - x + 3 y z - 3 y - z + 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
\(\displaystyle l_{27}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{2}}\boldsymbol{v}\cdot\left(\begin{array}{c}0\\0\\s_{1}\end{array}\right)\)
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \boldsymbol{\phi}_{27} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 12 y \left(- 3 x z + x - 3 y z + y + 3 z - 1\right)\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \boldsymbol{\phi}_{27} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 12 y \left(- 3 x z + x - 3 y z + y + 3 z - 1\right)\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
\(\displaystyle l_{28}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{3}}\boldsymbol{v}\cdot\left(\begin{array}{c}0\\0\\\frac{\sqrt{2} \left(1 - s_{1}\right)}{2}\end{array}\right)\)
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \boldsymbol{\phi}_{28} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 12 x y \left(2 - 3 z\right)\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \boldsymbol{\phi}_{28} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 12 x y \left(2 - 3 z\right)\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
\(\displaystyle l_{29}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{3}}\boldsymbol{v}\cdot\left(\begin{array}{c}\frac{\sqrt{2} \left(1 - s_{0}\right)}{2}\\\frac{\sqrt{2} \left(s_{0} - 1\right)}{2}\\0\end{array}\right)\)
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \boldsymbol{\phi}_{29} = \left(\begin{array}{c}\displaystyle 12 y z \left(- 4 x z + 4 x + z - 1\right)\\\displaystyle 24 x z \left(2 x z - 2 x - z + 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \boldsymbol{\phi}_{29} = \left(\begin{array}{c}\displaystyle 12 y z \left(- 4 x z + 4 x + z - 1\right)\\\displaystyle 24 x z \left(2 x z - 2 x - z + 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
\(\displaystyle l_{30}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{3}}\boldsymbol{v}\cdot\left(\begin{array}{c}\frac{\sqrt{2} s_{0}}{2}\\- \frac{\sqrt{2} s_{0}}{2}\\0\end{array}\right)\)
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \boldsymbol{\phi}_{30} = \left(\begin{array}{c}\displaystyle 24 y z \left(- 2 y z + 2 y + z - 1\right)\\\displaystyle 12 x z \left(4 y z - 4 y - z + 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \boldsymbol{\phi}_{30} = \left(\begin{array}{c}\displaystyle 24 y z \left(- 2 y z + 2 y + z - 1\right)\\\displaystyle 12 x z \left(4 y z - 4 y - z + 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
\(\displaystyle l_{31}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{3}}\boldsymbol{v}\cdot\left(\begin{array}{c}0\\0\\\frac{\sqrt{2} s_{1}}{2}\end{array}\right)\)
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \boldsymbol{\phi}_{31} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 12 x y \left(3 z - 1\right)\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \boldsymbol{\phi}_{31} = \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 12 x y \left(3 z - 1\right)\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
\(\displaystyle l_{32}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{4}}\boldsymbol{v}\cdot\left(\begin{array}{c}1\\0\\0\end{array}\right)\)
where \(f_{4}\) is the 4th face.
\(\displaystyle \boldsymbol{\phi}_{32} = \left(\begin{array}{c}\displaystyle 8 y z \left(- 3 x z + 2 x - 6 y z + 4 y + 6 z - 4\right)\\\displaystyle 8 x z \left(3 x z - 2 x + 6 y z - 4 y - 3 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 4 of the reference element.
where \(f_{4}\) is the 4th face.
\(\displaystyle \boldsymbol{\phi}_{32} = \left(\begin{array}{c}\displaystyle 8 y z \left(- 3 x z + 2 x - 6 y z + 4 y + 6 z - 4\right)\\\displaystyle 8 x z \left(3 x z - 2 x + 6 y z - 4 y - 3 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 4 of the reference element.
\(\displaystyle l_{33}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{4}}\boldsymbol{v}\cdot\left(\begin{array}{c}0\\1\\0\end{array}\right)\)
where \(f_{4}\) is the 4th face.
\(\displaystyle \boldsymbol{\phi}_{33} = \left(\begin{array}{c}\displaystyle 8 y z \left(6 x z - 4 x + 3 y z - 2 y - 3 z + 2\right)\\\displaystyle 8 x z \left(- 6 x z + 4 x - 3 y z + 2 y + 6 z - 4\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 4 of the reference element.
where \(f_{4}\) is the 4th face.
\(\displaystyle \boldsymbol{\phi}_{33} = \left(\begin{array}{c}\displaystyle 8 y z \left(6 x z - 4 x + 3 y z - 2 y - 3 z + 2\right)\\\displaystyle 8 x z \left(- 6 x z + 4 x - 3 y z + 2 y + 6 z - 4\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with face 4 of the reference element.
\(\displaystyle l_{34}:\mathbf{v}\mapsto\displaystyle\int_{R}\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)\cdot\mathbf{v}\)
where \(R\) is the reference element.
\(\displaystyle \boldsymbol{\phi}_{34} = \left(\begin{array}{c}\displaystyle 48 y z \left(x z - x + 2 y z - 2 y - 2 z + 2\right)\\\displaystyle 48 x z \left(- x z + x - 2 y z + 2 y + z - 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element.
\(\displaystyle \boldsymbol{\phi}_{34} = \left(\begin{array}{c}\displaystyle 48 y z \left(x z - x + 2 y z - 2 y - 2 z + 2\right)\\\displaystyle 48 x z \left(- x z + x - 2 y z + 2 y + z - 1\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
\(\displaystyle l_{35}:\mathbf{v}\mapsto\displaystyle\int_{R}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 1\\\displaystyle 0\end{array}\right)\cdot\mathbf{v}\)
where \(R\) is the reference element.
\(\displaystyle \boldsymbol{\phi}_{35} = \left(\begin{array}{c}\displaystyle 48 y z \left(- 2 x z + 2 x - y z + y + z - 1\right)\\\displaystyle 48 x z \left(2 x z - 2 x + y z - y - 2 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element.
\(\displaystyle \boldsymbol{\phi}_{35} = \left(\begin{array}{c}\displaystyle 48 y z \left(- 2 x z + 2 x - y z + y + z - 1\right)\\\displaystyle 48 x z \left(2 x z - 2 x + y z - y - 2 z + 2\right)\\\displaystyle 0\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.