an encyclopedia of finite element definitions
Degree 1 Gopalakrishnan–Lederer–Schöberl on a tetrahedron
◀ Back to Gopalakrishnan–Lederer–Schöberl definition page
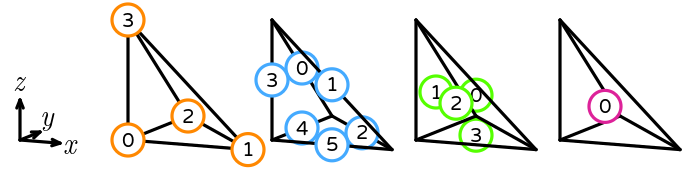
- \(R\) is the reference tetrahedron. The following numbering of the subentities of the reference is used:
- \(\mathcal{V}\) is spanned by: \(\left(\begin{array}{ccc}\displaystyle 1&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 1&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 1\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 1&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 1&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 1\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 1&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 1&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 1\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle x&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle x&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle x\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle x&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle x&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle x\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle x&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle x&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle x\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle y&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle y&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle y\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle y&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle y&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle y\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle y&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle y&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle y\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle z&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle z&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle z\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle z&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle z&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle z\\\displaystyle 0&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle z&\displaystyle 0&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle z&\displaystyle 0\end{array}\right)\), \(\left(\begin{array}{ccc}\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle z\end{array}\right)\)
- \(\mathcal{L}=\{l_0,...,l_{35}\}\)
- Functionals and basis functions:
\(\displaystyle l_{0}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{0}}(- s_{0} - s_{1} + 1)\left(\begin{array}{c}\displaystyle - \frac{2 \sqrt{3}}{3}\\\displaystyle \frac{2 \sqrt{3}}{3}\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle \frac{\sqrt{3}}{3}\\\displaystyle \frac{\sqrt{3}}{3}\\\displaystyle \frac{\sqrt{3}}{3}\end{array}\right)\)
where \(f_{0}\) is the 0th face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{0}\).
\(\displaystyle \mathbf{\Phi}_{0} = \left(\begin{array}{ccc}\displaystyle - \frac{390 x}{133} + \frac{214 y}{399} + \frac{116 z}{399} + \frac{8}{19}&\displaystyle \frac{107 y}{399}&\displaystyle \frac{58 z}{399}\\\displaystyle \frac{919 x}{399}&\displaystyle \frac{1838 x}{399} - \frac{180 y}{133} - \frac{458 z}{399} - \frac{8}{19}&\displaystyle - \frac{229 z}{399}\\\displaystyle - \frac{334 x}{399}&\displaystyle \frac{163 y}{399}&\displaystyle - \frac{668 x}{399} + \frac{326 y}{399} + \frac{6 z}{7}\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(f_{0}\) is the 0th face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{0}\).
\(\displaystyle \mathbf{\Phi}_{0} = \left(\begin{array}{ccc}\displaystyle - \frac{390 x}{133} + \frac{214 y}{399} + \frac{116 z}{399} + \frac{8}{19}&\displaystyle \frac{107 y}{399}&\displaystyle \frac{58 z}{399}\\\displaystyle \frac{919 x}{399}&\displaystyle \frac{1838 x}{399} - \frac{180 y}{133} - \frac{458 z}{399} - \frac{8}{19}&\displaystyle - \frac{229 z}{399}\\\displaystyle - \frac{334 x}{399}&\displaystyle \frac{163 y}{399}&\displaystyle - \frac{668 x}{399} + \frac{326 y}{399} + \frac{6 z}{7}\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{1}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{0}}(s_{0})\left(\begin{array}{c}\displaystyle - \frac{2 \sqrt{3}}{3}\\\displaystyle \frac{2 \sqrt{3}}{3}\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle \frac{\sqrt{3}}{3}\\\displaystyle \frac{\sqrt{3}}{3}\\\displaystyle \frac{\sqrt{3}}{3}\end{array}\right)\)
where \(f_{0}\) is the 0th face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{0}\).
\(\displaystyle \mathbf{\Phi}_{1} = \left(\begin{array}{ccc}\displaystyle \frac{66 x}{133} - \frac{390 y}{133} + \frac{44 z}{133} + \frac{8}{19}&\displaystyle - \frac{195 y}{133}&\displaystyle \frac{22 z}{133}\\\displaystyle - \frac{55 x}{133}&\displaystyle - \frac{110 x}{133} + \frac{780 y}{133} - \frac{110 z}{133} - \frac{16}{19}&\displaystyle - \frac{55 z}{133}\\\displaystyle \frac{22 x}{133}&\displaystyle - \frac{195 y}{133}&\displaystyle \frac{44 x}{133} - \frac{390 y}{133} + \frac{66 z}{133} + \frac{8}{19}\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(f_{0}\) is the 0th face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{0}\).
\(\displaystyle \mathbf{\Phi}_{1} = \left(\begin{array}{ccc}\displaystyle \frac{66 x}{133} - \frac{390 y}{133} + \frac{44 z}{133} + \frac{8}{19}&\displaystyle - \frac{195 y}{133}&\displaystyle \frac{22 z}{133}\\\displaystyle - \frac{55 x}{133}&\displaystyle - \frac{110 x}{133} + \frac{780 y}{133} - \frac{110 z}{133} - \frac{16}{19}&\displaystyle - \frac{55 z}{133}\\\displaystyle \frac{22 x}{133}&\displaystyle - \frac{195 y}{133}&\displaystyle \frac{44 x}{133} - \frac{390 y}{133} + \frac{66 z}{133} + \frac{8}{19}\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{2}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{0}}(s_{1})\left(\begin{array}{c}\displaystyle - \frac{2 \sqrt{3}}{3}\\\displaystyle \frac{2 \sqrt{3}}{3}\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle \frac{\sqrt{3}}{3}\\\displaystyle \frac{\sqrt{3}}{3}\\\displaystyle \frac{\sqrt{3}}{3}\end{array}\right)\)
where \(f_{0}\) is the 0th face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{0}\).
\(\displaystyle \mathbf{\Phi}_{2} = \left(\begin{array}{ccc}\displaystyle \frac{6 x}{7} + \frac{326 y}{399} - \frac{668 z}{399}&\displaystyle \frac{163 y}{399}&\displaystyle - \frac{334 z}{399}\\\displaystyle - \frac{229 x}{399}&\displaystyle - \frac{458 x}{399} - \frac{180 y}{133} + \frac{1838 z}{399} - \frac{8}{19}&\displaystyle \frac{919 z}{399}\\\displaystyle \frac{58 x}{399}&\displaystyle \frac{107 y}{399}&\displaystyle \frac{116 x}{399} + \frac{214 y}{399} - \frac{390 z}{133} + \frac{8}{19}\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(f_{0}\) is the 0th face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{0}\).
\(\displaystyle \mathbf{\Phi}_{2} = \left(\begin{array}{ccc}\displaystyle \frac{6 x}{7} + \frac{326 y}{399} - \frac{668 z}{399}&\displaystyle \frac{163 y}{399}&\displaystyle - \frac{334 z}{399}\\\displaystyle - \frac{229 x}{399}&\displaystyle - \frac{458 x}{399} - \frac{180 y}{133} + \frac{1838 z}{399} - \frac{8}{19}&\displaystyle \frac{919 z}{399}\\\displaystyle \frac{58 x}{399}&\displaystyle \frac{107 y}{399}&\displaystyle \frac{116 x}{399} + \frac{214 y}{399} - \frac{390 z}{133} + \frac{8}{19}\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{3}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{0}}(- s_{0} - s_{1} + 1)\left(\begin{array}{c}\displaystyle - \frac{2 \sqrt{3}}{3}\\\displaystyle 0\\\displaystyle \frac{2 \sqrt{3}}{3}\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle \frac{\sqrt{3}}{3}\\\displaystyle \frac{\sqrt{3}}{3}\\\displaystyle \frac{\sqrt{3}}{3}\end{array}\right)\)
where \(f_{0}\) is the 0th face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{0}\).
\(\displaystyle \mathbf{\Phi}_{3} = \left(\begin{array}{ccc}\displaystyle - \frac{390 x}{133} + \frac{116 y}{399} + \frac{214 z}{399} + \frac{8}{19}&\displaystyle \frac{58 y}{399}&\displaystyle \frac{107 z}{399}\\\displaystyle - \frac{334 x}{399}&\displaystyle - \frac{668 x}{399} + \frac{6 y}{7} + \frac{326 z}{399}&\displaystyle \frac{163 z}{399}\\\displaystyle \frac{919 x}{399}&\displaystyle - \frac{229 y}{399}&\displaystyle \frac{1838 x}{399} - \frac{458 y}{399} - \frac{180 z}{133} - \frac{8}{19}\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(f_{0}\) is the 0th face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{0}\).
\(\displaystyle \mathbf{\Phi}_{3} = \left(\begin{array}{ccc}\displaystyle - \frac{390 x}{133} + \frac{116 y}{399} + \frac{214 z}{399} + \frac{8}{19}&\displaystyle \frac{58 y}{399}&\displaystyle \frac{107 z}{399}\\\displaystyle - \frac{334 x}{399}&\displaystyle - \frac{668 x}{399} + \frac{6 y}{7} + \frac{326 z}{399}&\displaystyle \frac{163 z}{399}\\\displaystyle \frac{919 x}{399}&\displaystyle - \frac{229 y}{399}&\displaystyle \frac{1838 x}{399} - \frac{458 y}{399} - \frac{180 z}{133} - \frac{8}{19}\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{4}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{0}}(s_{0})\left(\begin{array}{c}\displaystyle - \frac{2 \sqrt{3}}{3}\\\displaystyle 0\\\displaystyle \frac{2 \sqrt{3}}{3}\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle \frac{\sqrt{3}}{3}\\\displaystyle \frac{\sqrt{3}}{3}\\\displaystyle \frac{\sqrt{3}}{3}\end{array}\right)\)
where \(f_{0}\) is the 0th face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{0}\).
\(\displaystyle \mathbf{\Phi}_{4} = \left(\begin{array}{ccc}\displaystyle \frac{6 x}{7} - \frac{668 y}{399} + \frac{326 z}{399}&\displaystyle - \frac{334 y}{399}&\displaystyle \frac{163 z}{399}\\\displaystyle \frac{58 x}{399}&\displaystyle \frac{116 x}{399} - \frac{390 y}{133} + \frac{214 z}{399} + \frac{8}{19}&\displaystyle \frac{107 z}{399}\\\displaystyle - \frac{229 x}{399}&\displaystyle \frac{919 y}{399}&\displaystyle - \frac{458 x}{399} + \frac{1838 y}{399} - \frac{180 z}{133} - \frac{8}{19}\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(f_{0}\) is the 0th face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{0}\).
\(\displaystyle \mathbf{\Phi}_{4} = \left(\begin{array}{ccc}\displaystyle \frac{6 x}{7} - \frac{668 y}{399} + \frac{326 z}{399}&\displaystyle - \frac{334 y}{399}&\displaystyle \frac{163 z}{399}\\\displaystyle \frac{58 x}{399}&\displaystyle \frac{116 x}{399} - \frac{390 y}{133} + \frac{214 z}{399} + \frac{8}{19}&\displaystyle \frac{107 z}{399}\\\displaystyle - \frac{229 x}{399}&\displaystyle \frac{919 y}{399}&\displaystyle - \frac{458 x}{399} + \frac{1838 y}{399} - \frac{180 z}{133} - \frac{8}{19}\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{5}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{0}}(s_{1})\left(\begin{array}{c}\displaystyle - \frac{2 \sqrt{3}}{3}\\\displaystyle 0\\\displaystyle \frac{2 \sqrt{3}}{3}\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle \frac{\sqrt{3}}{3}\\\displaystyle \frac{\sqrt{3}}{3}\\\displaystyle \frac{\sqrt{3}}{3}\end{array}\right)\)
where \(f_{0}\) is the 0th face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{0}\).
\(\displaystyle \mathbf{\Phi}_{5} = \left(\begin{array}{ccc}\displaystyle \frac{66 x}{133} + \frac{44 y}{133} - \frac{390 z}{133} + \frac{8}{19}&\displaystyle \frac{22 y}{133}&\displaystyle - \frac{195 z}{133}\\\displaystyle \frac{22 x}{133}&\displaystyle \frac{44 x}{133} + \frac{66 y}{133} - \frac{390 z}{133} + \frac{8}{19}&\displaystyle - \frac{195 z}{133}\\\displaystyle - \frac{55 x}{133}&\displaystyle - \frac{55 y}{133}&\displaystyle - \frac{110 x}{133} - \frac{110 y}{133} + \frac{780 z}{133} - \frac{16}{19}\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
where \(f_{0}\) is the 0th face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{0}\).
\(\displaystyle \mathbf{\Phi}_{5} = \left(\begin{array}{ccc}\displaystyle \frac{66 x}{133} + \frac{44 y}{133} - \frac{390 z}{133} + \frac{8}{19}&\displaystyle \frac{22 y}{133}&\displaystyle - \frac{195 z}{133}\\\displaystyle \frac{22 x}{133}&\displaystyle \frac{44 x}{133} + \frac{66 y}{133} - \frac{390 z}{133} + \frac{8}{19}&\displaystyle - \frac{195 z}{133}\\\displaystyle - \frac{55 x}{133}&\displaystyle - \frac{55 y}{133}&\displaystyle - \frac{110 x}{133} - \frac{110 y}{133} + \frac{780 z}{133} - \frac{16}{19}\end{array}\right)\)
This DOF is associated with face 0 of the reference element.
\(\displaystyle l_{6}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{1}}(- s_{0} - s_{1} + 1)\left(\begin{array}{c}\displaystyle 0\\\displaystyle 2\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \mathbf{\Phi}_{6} = \left(\begin{array}{ccc}\displaystyle - \frac{135 x}{133} - \frac{578 y}{399} - \frac{382 z}{399} + \frac{13}{19}&\displaystyle - \frac{289 y}{399}&\displaystyle - \frac{191 z}{399}\\\displaystyle - \frac{3845 x}{399} - 12 y - 12 z + 9&\displaystyle \frac{689 x}{399} + \frac{390 y}{133} + \frac{976 z}{399} - \frac{27}{19}&\displaystyle \frac{488 z}{399}\\\displaystyle - \frac{142 x}{399}&\displaystyle - \frac{296 y}{399}&\displaystyle - \frac{284 x}{399} - \frac{592 y}{399} - \frac{198 z}{133} + \frac{14}{19}\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \mathbf{\Phi}_{6} = \left(\begin{array}{ccc}\displaystyle - \frac{135 x}{133} - \frac{578 y}{399} - \frac{382 z}{399} + \frac{13}{19}&\displaystyle - \frac{289 y}{399}&\displaystyle - \frac{191 z}{399}\\\displaystyle - \frac{3845 x}{399} - 12 y - 12 z + 9&\displaystyle \frac{689 x}{399} + \frac{390 y}{133} + \frac{976 z}{399} - \frac{27}{19}&\displaystyle \frac{488 z}{399}\\\displaystyle - \frac{142 x}{399}&\displaystyle - \frac{296 y}{399}&\displaystyle - \frac{284 x}{399} - \frac{592 y}{399} - \frac{198 z}{133} + \frac{14}{19}\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
\(\displaystyle l_{7}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{1}}(s_{0})\left(\begin{array}{c}\displaystyle 0\\\displaystyle 2\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \mathbf{\Phi}_{7} = \left(\begin{array}{ccc}\displaystyle \frac{9 x}{133} + \frac{1222 y}{399} - \frac{94 z}{399} - \frac{11}{19}&\displaystyle \frac{611 y}{399}&\displaystyle - \frac{47 z}{399}\\\displaystyle \frac{583 x}{399} + 12 y - 3&\displaystyle - \frac{31 x}{399} - \frac{810 y}{133} + \frac{256 z}{399} + \frac{21}{19}&\displaystyle \frac{128 z}{399}\\\displaystyle \frac{2 x}{399}&\displaystyle \frac{604 y}{399}&\displaystyle \frac{4 x}{399} + \frac{1208 y}{399} - \frac{54 z}{133} - \frac{10}{19}\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \mathbf{\Phi}_{7} = \left(\begin{array}{ccc}\displaystyle \frac{9 x}{133} + \frac{1222 y}{399} - \frac{94 z}{399} - \frac{11}{19}&\displaystyle \frac{611 y}{399}&\displaystyle - \frac{47 z}{399}\\\displaystyle \frac{583 x}{399} + 12 y - 3&\displaystyle - \frac{31 x}{399} - \frac{810 y}{133} + \frac{256 z}{399} + \frac{21}{19}&\displaystyle \frac{128 z}{399}\\\displaystyle \frac{2 x}{399}&\displaystyle \frac{604 y}{399}&\displaystyle \frac{4 x}{399} + \frac{1208 y}{399} - \frac{54 z}{133} - \frac{10}{19}\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
\(\displaystyle l_{8}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{1}}(s_{1})\left(\begin{array}{c}\displaystyle 0\\\displaystyle 2\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \mathbf{\Phi}_{8} = \left(\begin{array}{ccc}\displaystyle - \frac{39 x}{133} - \frac{274 y}{399} + \frac{706 z}{399} - \frac{3}{19}&\displaystyle - \frac{137 y}{399}&\displaystyle \frac{353 z}{399}\\\displaystyle \frac{647 x}{399} + 12 z - 3&\displaystyle \frac{97 x}{399} + \frac{150 y}{133} - \frac{1912 z}{399} + \frac{13}{19}&\displaystyle - \frac{956 z}{399}\\\displaystyle \frac{10 x}{399}&\displaystyle - \frac{88 y}{399}&\displaystyle \frac{20 x}{399} - \frac{176 y}{399} + \frac{402 z}{133} - \frac{10}{19}\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \mathbf{\Phi}_{8} = \left(\begin{array}{ccc}\displaystyle - \frac{39 x}{133} - \frac{274 y}{399} + \frac{706 z}{399} - \frac{3}{19}&\displaystyle - \frac{137 y}{399}&\displaystyle \frac{353 z}{399}\\\displaystyle \frac{647 x}{399} + 12 z - 3&\displaystyle \frac{97 x}{399} + \frac{150 y}{133} - \frac{1912 z}{399} + \frac{13}{19}&\displaystyle - \frac{956 z}{399}\\\displaystyle \frac{10 x}{399}&\displaystyle - \frac{88 y}{399}&\displaystyle \frac{20 x}{399} - \frac{176 y}{399} + \frac{402 z}{133} - \frac{10}{19}\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
\(\displaystyle l_{9}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{1}}(- s_{0} - s_{1} + 1)\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \mathbf{\Phi}_{9} = \left(\begin{array}{ccc}\displaystyle - \frac{135 x}{133} - \frac{382 y}{399} - \frac{578 z}{399} + \frac{13}{19}&\displaystyle - \frac{191 y}{399}&\displaystyle - \frac{289 z}{399}\\\displaystyle - \frac{142 x}{399}&\displaystyle - \frac{284 x}{399} - \frac{198 y}{133} - \frac{592 z}{399} + \frac{14}{19}&\displaystyle - \frac{296 z}{399}\\\displaystyle - \frac{3845 x}{399} - 12 y - 12 z + 9&\displaystyle \frac{488 y}{399}&\displaystyle \frac{689 x}{399} + \frac{976 y}{399} + \frac{390 z}{133} - \frac{27}{19}\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \mathbf{\Phi}_{9} = \left(\begin{array}{ccc}\displaystyle - \frac{135 x}{133} - \frac{382 y}{399} - \frac{578 z}{399} + \frac{13}{19}&\displaystyle - \frac{191 y}{399}&\displaystyle - \frac{289 z}{399}\\\displaystyle - \frac{142 x}{399}&\displaystyle - \frac{284 x}{399} - \frac{198 y}{133} - \frac{592 z}{399} + \frac{14}{19}&\displaystyle - \frac{296 z}{399}\\\displaystyle - \frac{3845 x}{399} - 12 y - 12 z + 9&\displaystyle \frac{488 y}{399}&\displaystyle \frac{689 x}{399} + \frac{976 y}{399} + \frac{390 z}{133} - \frac{27}{19}\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
\(\displaystyle l_{10}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{1}}(s_{0})\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \mathbf{\Phi}_{10} = \left(\begin{array}{ccc}\displaystyle - \frac{39 x}{133} + \frac{706 y}{399} - \frac{274 z}{399} - \frac{3}{19}&\displaystyle \frac{353 y}{399}&\displaystyle - \frac{137 z}{399}\\\displaystyle \frac{10 x}{399}&\displaystyle \frac{20 x}{399} + \frac{402 y}{133} - \frac{176 z}{399} - \frac{10}{19}&\displaystyle - \frac{88 z}{399}\\\displaystyle \frac{647 x}{399} + 12 y - 3&\displaystyle - \frac{956 y}{399}&\displaystyle \frac{97 x}{399} - \frac{1912 y}{399} + \frac{150 z}{133} + \frac{13}{19}\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \mathbf{\Phi}_{10} = \left(\begin{array}{ccc}\displaystyle - \frac{39 x}{133} + \frac{706 y}{399} - \frac{274 z}{399} - \frac{3}{19}&\displaystyle \frac{353 y}{399}&\displaystyle - \frac{137 z}{399}\\\displaystyle \frac{10 x}{399}&\displaystyle \frac{20 x}{399} + \frac{402 y}{133} - \frac{176 z}{399} - \frac{10}{19}&\displaystyle - \frac{88 z}{399}\\\displaystyle \frac{647 x}{399} + 12 y - 3&\displaystyle - \frac{956 y}{399}&\displaystyle \frac{97 x}{399} - \frac{1912 y}{399} + \frac{150 z}{133} + \frac{13}{19}\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
\(\displaystyle l_{11}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{1}}(s_{1})\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)\)
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \mathbf{\Phi}_{11} = \left(\begin{array}{ccc}\displaystyle \frac{9 x}{133} - \frac{94 y}{399} + \frac{1222 z}{399} - \frac{11}{19}&\displaystyle - \frac{47 y}{399}&\displaystyle \frac{611 z}{399}\\\displaystyle \frac{2 x}{399}&\displaystyle \frac{4 x}{399} - \frac{54 y}{133} + \frac{1208 z}{399} - \frac{10}{19}&\displaystyle \frac{604 z}{399}\\\displaystyle \frac{583 x}{399} + 12 z - 3&\displaystyle \frac{128 y}{399}&\displaystyle - \frac{31 x}{399} + \frac{256 y}{399} - \frac{810 z}{133} + \frac{21}{19}\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
where \(f_{1}\) is the 1st face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{1}\).
\(\displaystyle \mathbf{\Phi}_{11} = \left(\begin{array}{ccc}\displaystyle \frac{9 x}{133} - \frac{94 y}{399} + \frac{1222 z}{399} - \frac{11}{19}&\displaystyle - \frac{47 y}{399}&\displaystyle \frac{611 z}{399}\\\displaystyle \frac{2 x}{399}&\displaystyle \frac{4 x}{399} - \frac{54 y}{133} + \frac{1208 z}{399} - \frac{10}{19}&\displaystyle \frac{604 z}{399}\\\displaystyle \frac{583 x}{399} + 12 z - 3&\displaystyle \frac{128 y}{399}&\displaystyle - \frac{31 x}{399} + \frac{256 y}{399} - \frac{810 z}{133} + \frac{21}{19}\end{array}\right)\)
This DOF is associated with face 1 of the reference element.
\(\displaystyle l_{12}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{2}}(- s_{0} - s_{1} + 1)\left(\begin{array}{c}\displaystyle 2\\\displaystyle 0\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle -1\\\displaystyle 0\end{array}\right)\)
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \mathbf{\Phi}_{12} = \left(\begin{array}{ccc}\displaystyle - \frac{390 x}{133} - \frac{689 y}{399} - \frac{976 z}{399} + \frac{27}{19}&\displaystyle 12 x + \frac{3845 y}{399} + 12 z - 9&\displaystyle - \frac{488 z}{399}\\\displaystyle \frac{289 x}{399}&\displaystyle \frac{578 x}{399} + \frac{135 y}{133} + \frac{382 z}{399} - \frac{13}{19}&\displaystyle \frac{191 z}{399}\\\displaystyle \frac{296 x}{399}&\displaystyle \frac{142 y}{399}&\displaystyle \frac{592 x}{399} + \frac{284 y}{399} + \frac{198 z}{133} - \frac{14}{19}\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \mathbf{\Phi}_{12} = \left(\begin{array}{ccc}\displaystyle - \frac{390 x}{133} - \frac{689 y}{399} - \frac{976 z}{399} + \frac{27}{19}&\displaystyle 12 x + \frac{3845 y}{399} + 12 z - 9&\displaystyle - \frac{488 z}{399}\\\displaystyle \frac{289 x}{399}&\displaystyle \frac{578 x}{399} + \frac{135 y}{133} + \frac{382 z}{399} - \frac{13}{19}&\displaystyle \frac{191 z}{399}\\\displaystyle \frac{296 x}{399}&\displaystyle \frac{142 y}{399}&\displaystyle \frac{592 x}{399} + \frac{284 y}{399} + \frac{198 z}{133} - \frac{14}{19}\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
\(\displaystyle l_{13}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{2}}(s_{0})\left(\begin{array}{c}\displaystyle 2\\\displaystyle 0\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle -1\\\displaystyle 0\end{array}\right)\)
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \mathbf{\Phi}_{13} = \left(\begin{array}{ccc}\displaystyle \frac{810 x}{133} + \frac{31 y}{399} - \frac{256 z}{399} - \frac{21}{19}&\displaystyle - 12 x - \frac{583 y}{399} + 3&\displaystyle - \frac{128 z}{399}\\\displaystyle - \frac{611 x}{399}&\displaystyle - \frac{1222 x}{399} - \frac{9 y}{133} + \frac{94 z}{399} + \frac{11}{19}&\displaystyle \frac{47 z}{399}\\\displaystyle - \frac{604 x}{399}&\displaystyle - \frac{2 y}{399}&\displaystyle - \frac{1208 x}{399} - \frac{4 y}{399} + \frac{54 z}{133} + \frac{10}{19}\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \mathbf{\Phi}_{13} = \left(\begin{array}{ccc}\displaystyle \frac{810 x}{133} + \frac{31 y}{399} - \frac{256 z}{399} - \frac{21}{19}&\displaystyle - 12 x - \frac{583 y}{399} + 3&\displaystyle - \frac{128 z}{399}\\\displaystyle - \frac{611 x}{399}&\displaystyle - \frac{1222 x}{399} - \frac{9 y}{133} + \frac{94 z}{399} + \frac{11}{19}&\displaystyle \frac{47 z}{399}\\\displaystyle - \frac{604 x}{399}&\displaystyle - \frac{2 y}{399}&\displaystyle - \frac{1208 x}{399} - \frac{4 y}{399} + \frac{54 z}{133} + \frac{10}{19}\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
\(\displaystyle l_{14}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{2}}(s_{1})\left(\begin{array}{c}\displaystyle 2\\\displaystyle 0\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle -1\\\displaystyle 0\end{array}\right)\)
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \mathbf{\Phi}_{14} = \left(\begin{array}{ccc}\displaystyle - \frac{150 x}{133} - \frac{97 y}{399} + \frac{1912 z}{399} - \frac{13}{19}&\displaystyle - \frac{647 y}{399} - 12 z + 3&\displaystyle \frac{956 z}{399}\\\displaystyle \frac{137 x}{399}&\displaystyle \frac{274 x}{399} + \frac{39 y}{133} - \frac{706 z}{399} + \frac{3}{19}&\displaystyle - \frac{353 z}{399}\\\displaystyle \frac{88 x}{399}&\displaystyle - \frac{10 y}{399}&\displaystyle \frac{176 x}{399} - \frac{20 y}{399} - \frac{402 z}{133} + \frac{10}{19}\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \mathbf{\Phi}_{14} = \left(\begin{array}{ccc}\displaystyle - \frac{150 x}{133} - \frac{97 y}{399} + \frac{1912 z}{399} - \frac{13}{19}&\displaystyle - \frac{647 y}{399} - 12 z + 3&\displaystyle \frac{956 z}{399}\\\displaystyle \frac{137 x}{399}&\displaystyle \frac{274 x}{399} + \frac{39 y}{133} - \frac{706 z}{399} + \frac{3}{19}&\displaystyle - \frac{353 z}{399}\\\displaystyle \frac{88 x}{399}&\displaystyle - \frac{10 y}{399}&\displaystyle \frac{176 x}{399} - \frac{20 y}{399} - \frac{402 z}{133} + \frac{10}{19}\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
\(\displaystyle l_{15}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{2}}(- s_{0} - s_{1} + 1)\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle -1\\\displaystyle 0\end{array}\right)\)
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \mathbf{\Phi}_{15} = \left(\begin{array}{ccc}\displaystyle \frac{198 x}{133} + \frac{284 y}{399} + \frac{592 z}{399} - \frac{14}{19}&\displaystyle \frac{142 y}{399}&\displaystyle \frac{296 z}{399}\\\displaystyle \frac{191 x}{399}&\displaystyle \frac{382 x}{399} + \frac{135 y}{133} + \frac{578 z}{399} - \frac{13}{19}&\displaystyle \frac{289 z}{399}\\\displaystyle - \frac{488 x}{399}&\displaystyle 12 x + \frac{3845 y}{399} + 12 z - 9&\displaystyle - \frac{976 x}{399} - \frac{689 y}{399} - \frac{390 z}{133} + \frac{27}{19}\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \mathbf{\Phi}_{15} = \left(\begin{array}{ccc}\displaystyle \frac{198 x}{133} + \frac{284 y}{399} + \frac{592 z}{399} - \frac{14}{19}&\displaystyle \frac{142 y}{399}&\displaystyle \frac{296 z}{399}\\\displaystyle \frac{191 x}{399}&\displaystyle \frac{382 x}{399} + \frac{135 y}{133} + \frac{578 z}{399} - \frac{13}{19}&\displaystyle \frac{289 z}{399}\\\displaystyle - \frac{488 x}{399}&\displaystyle 12 x + \frac{3845 y}{399} + 12 z - 9&\displaystyle - \frac{976 x}{399} - \frac{689 y}{399} - \frac{390 z}{133} + \frac{27}{19}\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
\(\displaystyle l_{16}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{2}}(s_{0})\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle -1\\\displaystyle 0\end{array}\right)\)
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \mathbf{\Phi}_{16} = \left(\begin{array}{ccc}\displaystyle - \frac{402 x}{133} - \frac{20 y}{399} + \frac{176 z}{399} + \frac{10}{19}&\displaystyle - \frac{10 y}{399}&\displaystyle \frac{88 z}{399}\\\displaystyle - \frac{353 x}{399}&\displaystyle - \frac{706 x}{399} + \frac{39 y}{133} + \frac{274 z}{399} + \frac{3}{19}&\displaystyle \frac{137 z}{399}\\\displaystyle \frac{956 x}{399}&\displaystyle - 12 x - \frac{647 y}{399} + 3&\displaystyle \frac{1912 x}{399} - \frac{97 y}{399} - \frac{150 z}{133} - \frac{13}{19}\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \mathbf{\Phi}_{16} = \left(\begin{array}{ccc}\displaystyle - \frac{402 x}{133} - \frac{20 y}{399} + \frac{176 z}{399} + \frac{10}{19}&\displaystyle - \frac{10 y}{399}&\displaystyle \frac{88 z}{399}\\\displaystyle - \frac{353 x}{399}&\displaystyle - \frac{706 x}{399} + \frac{39 y}{133} + \frac{274 z}{399} + \frac{3}{19}&\displaystyle \frac{137 z}{399}\\\displaystyle \frac{956 x}{399}&\displaystyle - 12 x - \frac{647 y}{399} + 3&\displaystyle \frac{1912 x}{399} - \frac{97 y}{399} - \frac{150 z}{133} - \frac{13}{19}\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
\(\displaystyle l_{17}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{2}}(s_{1})\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle -1\\\displaystyle 0\end{array}\right)\)
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \mathbf{\Phi}_{17} = \left(\begin{array}{ccc}\displaystyle \frac{54 x}{133} - \frac{4 y}{399} - \frac{1208 z}{399} + \frac{10}{19}&\displaystyle - \frac{2 y}{399}&\displaystyle - \frac{604 z}{399}\\\displaystyle \frac{47 x}{399}&\displaystyle \frac{94 x}{399} - \frac{9 y}{133} - \frac{1222 z}{399} + \frac{11}{19}&\displaystyle - \frac{611 z}{399}\\\displaystyle - \frac{128 x}{399}&\displaystyle - \frac{583 y}{399} - 12 z + 3&\displaystyle - \frac{256 x}{399} + \frac{31 y}{399} + \frac{810 z}{133} - \frac{21}{19}\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
where \(f_{2}\) is the 2nd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{2}\).
\(\displaystyle \mathbf{\Phi}_{17} = \left(\begin{array}{ccc}\displaystyle \frac{54 x}{133} - \frac{4 y}{399} - \frac{1208 z}{399} + \frac{10}{19}&\displaystyle - \frac{2 y}{399}&\displaystyle - \frac{604 z}{399}\\\displaystyle \frac{47 x}{399}&\displaystyle \frac{94 x}{399} - \frac{9 y}{133} - \frac{1222 z}{399} + \frac{11}{19}&\displaystyle - \frac{611 z}{399}\\\displaystyle - \frac{128 x}{399}&\displaystyle - \frac{583 y}{399} - 12 z + 3&\displaystyle - \frac{256 x}{399} + \frac{31 y}{399} + \frac{810 z}{133} - \frac{21}{19}\end{array}\right)\)
This DOF is associated with face 2 of the reference element.
\(\displaystyle l_{18}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{3}}(- s_{0} - s_{1} + 1)\left(\begin{array}{c}\displaystyle 2\\\displaystyle 0\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 1\end{array}\right)\)
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \mathbf{\Phi}_{18} = \left(\begin{array}{ccc}\displaystyle \frac{390 x}{133} + \frac{976 y}{399} + \frac{689 z}{399} - \frac{27}{19}&\displaystyle \frac{488 y}{399}&\displaystyle - 12 x - 12 y - \frac{3845 z}{399} + 9\\\displaystyle - \frac{296 x}{399}&\displaystyle - \frac{592 x}{399} - \frac{198 y}{133} - \frac{284 z}{399} + \frac{14}{19}&\displaystyle - \frac{142 z}{399}\\\displaystyle - \frac{289 x}{399}&\displaystyle - \frac{191 y}{399}&\displaystyle - \frac{578 x}{399} - \frac{382 y}{399} - \frac{135 z}{133} + \frac{13}{19}\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \mathbf{\Phi}_{18} = \left(\begin{array}{ccc}\displaystyle \frac{390 x}{133} + \frac{976 y}{399} + \frac{689 z}{399} - \frac{27}{19}&\displaystyle \frac{488 y}{399}&\displaystyle - 12 x - 12 y - \frac{3845 z}{399} + 9\\\displaystyle - \frac{296 x}{399}&\displaystyle - \frac{592 x}{399} - \frac{198 y}{133} - \frac{284 z}{399} + \frac{14}{19}&\displaystyle - \frac{142 z}{399}\\\displaystyle - \frac{289 x}{399}&\displaystyle - \frac{191 y}{399}&\displaystyle - \frac{578 x}{399} - \frac{382 y}{399} - \frac{135 z}{133} + \frac{13}{19}\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
\(\displaystyle l_{19}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{3}}(s_{0})\left(\begin{array}{c}\displaystyle 2\\\displaystyle 0\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 1\end{array}\right)\)
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \mathbf{\Phi}_{19} = \left(\begin{array}{ccc}\displaystyle - \frac{810 x}{133} + \frac{256 y}{399} - \frac{31 z}{399} + \frac{21}{19}&\displaystyle \frac{128 y}{399}&\displaystyle 12 x + \frac{583 z}{399} - 3\\\displaystyle \frac{604 x}{399}&\displaystyle \frac{1208 x}{399} - \frac{54 y}{133} + \frac{4 z}{399} - \frac{10}{19}&\displaystyle \frac{2 z}{399}\\\displaystyle \frac{611 x}{399}&\displaystyle - \frac{47 y}{399}&\displaystyle \frac{1222 x}{399} - \frac{94 y}{399} + \frac{9 z}{133} - \frac{11}{19}\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \mathbf{\Phi}_{19} = \left(\begin{array}{ccc}\displaystyle - \frac{810 x}{133} + \frac{256 y}{399} - \frac{31 z}{399} + \frac{21}{19}&\displaystyle \frac{128 y}{399}&\displaystyle 12 x + \frac{583 z}{399} - 3\\\displaystyle \frac{604 x}{399}&\displaystyle \frac{1208 x}{399} - \frac{54 y}{133} + \frac{4 z}{399} - \frac{10}{19}&\displaystyle \frac{2 z}{399}\\\displaystyle \frac{611 x}{399}&\displaystyle - \frac{47 y}{399}&\displaystyle \frac{1222 x}{399} - \frac{94 y}{399} + \frac{9 z}{133} - \frac{11}{19}\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
\(\displaystyle l_{20}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{3}}(s_{1})\left(\begin{array}{c}\displaystyle 2\\\displaystyle 0\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 1\end{array}\right)\)
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \mathbf{\Phi}_{20} = \left(\begin{array}{ccc}\displaystyle \frac{150 x}{133} - \frac{1912 y}{399} + \frac{97 z}{399} + \frac{13}{19}&\displaystyle - \frac{956 y}{399}&\displaystyle 12 y + \frac{647 z}{399} - 3\\\displaystyle - \frac{88 x}{399}&\displaystyle - \frac{176 x}{399} + \frac{402 y}{133} + \frac{20 z}{399} - \frac{10}{19}&\displaystyle \frac{10 z}{399}\\\displaystyle - \frac{137 x}{399}&\displaystyle \frac{353 y}{399}&\displaystyle - \frac{274 x}{399} + \frac{706 y}{399} - \frac{39 z}{133} - \frac{3}{19}\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \mathbf{\Phi}_{20} = \left(\begin{array}{ccc}\displaystyle \frac{150 x}{133} - \frac{1912 y}{399} + \frac{97 z}{399} + \frac{13}{19}&\displaystyle - \frac{956 y}{399}&\displaystyle 12 y + \frac{647 z}{399} - 3\\\displaystyle - \frac{88 x}{399}&\displaystyle - \frac{176 x}{399} + \frac{402 y}{133} + \frac{20 z}{399} - \frac{10}{19}&\displaystyle \frac{10 z}{399}\\\displaystyle - \frac{137 x}{399}&\displaystyle \frac{353 y}{399}&\displaystyle - \frac{274 x}{399} + \frac{706 y}{399} - \frac{39 z}{133} - \frac{3}{19}\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
\(\displaystyle l_{21}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{3}}(- s_{0} - s_{1} + 1)\left(\begin{array}{c}\displaystyle 0\\\displaystyle 2\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 1\end{array}\right)\)
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \mathbf{\Phi}_{21} = \left(\begin{array}{ccc}\displaystyle - \frac{198 x}{133} - \frac{592 y}{399} - \frac{284 z}{399} + \frac{14}{19}&\displaystyle - \frac{296 y}{399}&\displaystyle - \frac{142 z}{399}\\\displaystyle \frac{488 x}{399}&\displaystyle \frac{976 x}{399} + \frac{390 y}{133} + \frac{689 z}{399} - \frac{27}{19}&\displaystyle - 12 x - 12 y - \frac{3845 z}{399} + 9\\\displaystyle - \frac{191 x}{399}&\displaystyle - \frac{289 y}{399}&\displaystyle - \frac{382 x}{399} - \frac{578 y}{399} - \frac{135 z}{133} + \frac{13}{19}\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \mathbf{\Phi}_{21} = \left(\begin{array}{ccc}\displaystyle - \frac{198 x}{133} - \frac{592 y}{399} - \frac{284 z}{399} + \frac{14}{19}&\displaystyle - \frac{296 y}{399}&\displaystyle - \frac{142 z}{399}\\\displaystyle \frac{488 x}{399}&\displaystyle \frac{976 x}{399} + \frac{390 y}{133} + \frac{689 z}{399} - \frac{27}{19}&\displaystyle - 12 x - 12 y - \frac{3845 z}{399} + 9\\\displaystyle - \frac{191 x}{399}&\displaystyle - \frac{289 y}{399}&\displaystyle - \frac{382 x}{399} - \frac{578 y}{399} - \frac{135 z}{133} + \frac{13}{19}\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
\(\displaystyle l_{22}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{3}}(s_{0})\left(\begin{array}{c}\displaystyle 0\\\displaystyle 2\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 1\end{array}\right)\)
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \mathbf{\Phi}_{22} = \left(\begin{array}{ccc}\displaystyle \frac{402 x}{133} - \frac{176 y}{399} + \frac{20 z}{399} - \frac{10}{19}&\displaystyle - \frac{88 y}{399}&\displaystyle \frac{10 z}{399}\\\displaystyle - \frac{956 x}{399}&\displaystyle - \frac{1912 x}{399} + \frac{150 y}{133} + \frac{97 z}{399} + \frac{13}{19}&\displaystyle 12 x + \frac{647 z}{399} - 3\\\displaystyle \frac{353 x}{399}&\displaystyle - \frac{137 y}{399}&\displaystyle \frac{706 x}{399} - \frac{274 y}{399} - \frac{39 z}{133} - \frac{3}{19}\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \mathbf{\Phi}_{22} = \left(\begin{array}{ccc}\displaystyle \frac{402 x}{133} - \frac{176 y}{399} + \frac{20 z}{399} - \frac{10}{19}&\displaystyle - \frac{88 y}{399}&\displaystyle \frac{10 z}{399}\\\displaystyle - \frac{956 x}{399}&\displaystyle - \frac{1912 x}{399} + \frac{150 y}{133} + \frac{97 z}{399} + \frac{13}{19}&\displaystyle 12 x + \frac{647 z}{399} - 3\\\displaystyle \frac{353 x}{399}&\displaystyle - \frac{137 y}{399}&\displaystyle \frac{706 x}{399} - \frac{274 y}{399} - \frac{39 z}{133} - \frac{3}{19}\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
\(\displaystyle l_{23}:\boldsymbol{V}\mapsto\displaystyle\int_{f_{3}}(s_{1})\left(\begin{array}{c}\displaystyle 0\\\displaystyle 2\\\displaystyle 0\end{array}\right)^{\text{t}}\boldsymbol{V}\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 1\end{array}\right)\)
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \mathbf{\Phi}_{23} = \left(\begin{array}{ccc}\displaystyle - \frac{54 x}{133} + \frac{1208 y}{399} + \frac{4 z}{399} - \frac{10}{19}&\displaystyle \frac{604 y}{399}&\displaystyle \frac{2 z}{399}\\\displaystyle \frac{128 x}{399}&\displaystyle \frac{256 x}{399} - \frac{810 y}{133} - \frac{31 z}{399} + \frac{21}{19}&\displaystyle 12 y + \frac{583 z}{399} - 3\\\displaystyle - \frac{47 x}{399}&\displaystyle \frac{611 y}{399}&\displaystyle - \frac{94 x}{399} + \frac{1222 y}{399} + \frac{9 z}{133} - \frac{11}{19}\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
where \(f_{3}\) is the 3rd face;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(f_{3}\).
\(\displaystyle \mathbf{\Phi}_{23} = \left(\begin{array}{ccc}\displaystyle - \frac{54 x}{133} + \frac{1208 y}{399} + \frac{4 z}{399} - \frac{10}{19}&\displaystyle \frac{604 y}{399}&\displaystyle \frac{2 z}{399}\\\displaystyle \frac{128 x}{399}&\displaystyle \frac{256 x}{399} - \frac{810 y}{133} - \frac{31 z}{399} + \frac{21}{19}&\displaystyle 12 y + \frac{583 z}{399} - 3\\\displaystyle - \frac{47 x}{399}&\displaystyle \frac{611 y}{399}&\displaystyle - \frac{94 x}{399} + \frac{1222 y}{399} + \frac{9 z}{133} - \frac{11}{19}\end{array}\right)\)
This DOF is associated with face 3 of the reference element.
\(\displaystyle l_{24}:\boldsymbol{V}\mapsto\displaystyle\int_{R}\operatorname{tr}(\boldsymbol{V})(- s_{0} - s_{1} - s_{2} + 1)\)
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{24} = \left(\begin{array}{ccc}\displaystyle - 40 x - 40 y - 40 z + 32&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle - 40 x - 40 y - 40 z + 32&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle - 40 x - 40 y - 40 z + 32\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{24} = \left(\begin{array}{ccc}\displaystyle - 40 x - 40 y - 40 z + 32&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle - 40 x - 40 y - 40 z + 32&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle - 40 x - 40 y - 40 z + 32\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
\(\displaystyle l_{25}:\boldsymbol{V}\mapsto\displaystyle\int_{R}\operatorname{tr}(\boldsymbol{V})(s_{0})\)
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{25} = \left(\begin{array}{ccc}\displaystyle 40 x - 8&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 40 x - 8&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 40 x - 8\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{25} = \left(\begin{array}{ccc}\displaystyle 40 x - 8&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 40 x - 8&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 40 x - 8\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
\(\displaystyle l_{26}:\boldsymbol{V}\mapsto\displaystyle\int_{R}\operatorname{tr}(\boldsymbol{V})(s_{1})\)
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{26} = \left(\begin{array}{ccc}\displaystyle 40 y - 8&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 40 y - 8&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 40 y - 8\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{26} = \left(\begin{array}{ccc}\displaystyle 40 y - 8&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 40 y - 8&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 40 y - 8\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
\(\displaystyle l_{27}:\boldsymbol{V}\mapsto\displaystyle\int_{R}\operatorname{tr}(\boldsymbol{V})(s_{2})\)
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{27} = \left(\begin{array}{ccc}\displaystyle 40 z - 8&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 40 z - 8&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 40 z - 8\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{27} = \left(\begin{array}{ccc}\displaystyle 40 z - 8&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle 40 z - 8&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle 40 z - 8\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
\(\displaystyle l_{28}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{ccc}\displaystyle - \frac{2 s_{0}}{3} - \frac{2 s_{1}}{3} - \frac{2 s_{2}}{3} + \frac{2}{3}&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle \frac{s_{0}}{3} + \frac{s_{1}}{3} + \frac{s_{2}}{3} - \frac{1}{3}&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle \frac{s_{0}}{3} + \frac{s_{1}}{3} + \frac{s_{2}}{3} - \frac{1}{3}\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{28} = \left(\begin{array}{ccc}\displaystyle - \frac{1560 x}{19} - \frac{1720 y}{19} - \frac{1640 z}{19} + \frac{1440}{19}&\displaystyle \frac{280 y}{19}&\displaystyle \frac{320 z}{19}\\\displaystyle - \frac{40 x}{19}&\displaystyle - \frac{80 x}{19} + \frac{80 z}{19}&\displaystyle \frac{40 z}{19}\\\displaystyle - \frac{320 x}{19}&\displaystyle - \frac{280 y}{19}&\displaystyle \frac{1640 x}{19} + \frac{1720 y}{19} + \frac{1560 z}{19} - \frac{1440}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{28} = \left(\begin{array}{ccc}\displaystyle - \frac{1560 x}{19} - \frac{1720 y}{19} - \frac{1640 z}{19} + \frac{1440}{19}&\displaystyle \frac{280 y}{19}&\displaystyle \frac{320 z}{19}\\\displaystyle - \frac{40 x}{19}&\displaystyle - \frac{80 x}{19} + \frac{80 z}{19}&\displaystyle \frac{40 z}{19}\\\displaystyle - \frac{320 x}{19}&\displaystyle - \frac{280 y}{19}&\displaystyle \frac{1640 x}{19} + \frac{1720 y}{19} + \frac{1560 z}{19} - \frac{1440}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
\(\displaystyle l_{29}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{ccc}\displaystyle \frac{s_{0}}{3} + \frac{s_{1}}{3} + \frac{s_{2}}{3} - \frac{1}{3}&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle - \frac{2 s_{0}}{3} - \frac{2 s_{1}}{3} - \frac{2 s_{2}}{3} + \frac{2}{3}&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle \frac{s_{0}}{3} + \frac{s_{1}}{3} + \frac{s_{2}}{3} - \frac{1}{3}\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{29} = \left(\begin{array}{ccc}\displaystyle - \frac{80 y}{19} + \frac{80 z}{19}&\displaystyle - \frac{40 y}{19}&\displaystyle \frac{40 z}{19}\\\displaystyle \frac{280 x}{19}&\displaystyle - \frac{1720 x}{19} - \frac{1560 y}{19} - \frac{1640 z}{19} + \frac{1440}{19}&\displaystyle \frac{320 z}{19}\\\displaystyle - \frac{280 x}{19}&\displaystyle - \frac{320 y}{19}&\displaystyle \frac{1720 x}{19} + \frac{1640 y}{19} + \frac{1560 z}{19} - \frac{1440}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{29} = \left(\begin{array}{ccc}\displaystyle - \frac{80 y}{19} + \frac{80 z}{19}&\displaystyle - \frac{40 y}{19}&\displaystyle \frac{40 z}{19}\\\displaystyle \frac{280 x}{19}&\displaystyle - \frac{1720 x}{19} - \frac{1560 y}{19} - \frac{1640 z}{19} + \frac{1440}{19}&\displaystyle \frac{320 z}{19}\\\displaystyle - \frac{280 x}{19}&\displaystyle - \frac{320 y}{19}&\displaystyle \frac{1720 x}{19} + \frac{1640 y}{19} + \frac{1560 z}{19} - \frac{1440}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
\(\displaystyle l_{30}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{ccc}\displaystyle \frac{s_{0}}{3}&\displaystyle 0&\displaystyle 0\\\displaystyle s_{0}&\displaystyle - \frac{2 s_{0}}{3}&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle \frac{s_{0}}{3}\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{30} = \left(\begin{array}{ccc}\displaystyle \frac{3000 x}{133} + \frac{2080 y}{399} + \frac{80 z}{21} - \frac{120}{19}&\displaystyle \frac{1040 y}{399}&\displaystyle \frac{40 z}{21}\\\displaystyle \frac{880 x}{21}&\displaystyle - \frac{760 x}{21} - \frac{1200 y}{133} - \frac{2960 z}{399} + \frac{200}{19}&\displaystyle - \frac{1480 z}{399}\\\displaystyle \frac{2720 x}{399}&\displaystyle \frac{40 y}{21}&\displaystyle \frac{5440 x}{399} + \frac{80 y}{21} + \frac{480 z}{133} - \frac{80}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{30} = \left(\begin{array}{ccc}\displaystyle \frac{3000 x}{133} + \frac{2080 y}{399} + \frac{80 z}{21} - \frac{120}{19}&\displaystyle \frac{1040 y}{399}&\displaystyle \frac{40 z}{21}\\\displaystyle \frac{880 x}{21}&\displaystyle - \frac{760 x}{21} - \frac{1200 y}{133} - \frac{2960 z}{399} + \frac{200}{19}&\displaystyle - \frac{1480 z}{399}\\\displaystyle \frac{2720 x}{399}&\displaystyle \frac{40 y}{21}&\displaystyle \frac{5440 x}{399} + \frac{80 y}{21} + \frac{480 z}{133} - \frac{80}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
\(\displaystyle l_{31}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{ccc}\displaystyle \frac{s_{0}}{3}&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle \frac{s_{0}}{3}&\displaystyle 0\\\displaystyle s_{0}&\displaystyle 0&\displaystyle - \frac{2 s_{0}}{3}\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{31} = \left(\begin{array}{ccc}\displaystyle \frac{3000 x}{133} + \frac{80 y}{21} + \frac{2080 z}{399} - \frac{120}{19}&\displaystyle \frac{40 y}{21}&\displaystyle \frac{1040 z}{399}\\\displaystyle \frac{2720 x}{399}&\displaystyle \frac{5440 x}{399} + \frac{480 y}{133} + \frac{80 z}{21} - \frac{80}{19}&\displaystyle \frac{40 z}{21}\\\displaystyle \frac{880 x}{21}&\displaystyle - \frac{1480 y}{399}&\displaystyle - \frac{760 x}{21} - \frac{2960 y}{399} - \frac{1200 z}{133} + \frac{200}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{31} = \left(\begin{array}{ccc}\displaystyle \frac{3000 x}{133} + \frac{80 y}{21} + \frac{2080 z}{399} - \frac{120}{19}&\displaystyle \frac{40 y}{21}&\displaystyle \frac{1040 z}{399}\\\displaystyle \frac{2720 x}{399}&\displaystyle \frac{5440 x}{399} + \frac{480 y}{133} + \frac{80 z}{21} - \frac{80}{19}&\displaystyle \frac{40 z}{21}\\\displaystyle \frac{880 x}{21}&\displaystyle - \frac{1480 y}{399}&\displaystyle - \frac{760 x}{21} - \frac{2960 y}{399} - \frac{1200 z}{133} + \frac{200}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
\(\displaystyle l_{32}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{ccc}\displaystyle - \frac{s_{1}}{3}&\displaystyle 0&\displaystyle 0\\\displaystyle 0&\displaystyle - \frac{s_{1}}{3}&\displaystyle 0\\\displaystyle 0&\displaystyle - s_{1}&\displaystyle \frac{2 s_{1}}{3}\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{32} = \left(\begin{array}{ccc}\displaystyle - \frac{240 x}{19} - \frac{2840 y}{57} - \frac{640 z}{57} + \frac{280}{19}&\displaystyle \frac{2000 y}{57}&\displaystyle - \frac{320 z}{57}\\\displaystyle \frac{40 x}{57}&\displaystyle \frac{80 x}{57} - \frac{80 z}{57}&\displaystyle - \frac{40 z}{57}\\\displaystyle \frac{320 x}{57}&\displaystyle - \frac{2000 y}{57}&\displaystyle \frac{640 x}{57} + \frac{2840 y}{57} + \frac{240 z}{19} - \frac{280}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{32} = \left(\begin{array}{ccc}\displaystyle - \frac{240 x}{19} - \frac{2840 y}{57} - \frac{640 z}{57} + \frac{280}{19}&\displaystyle \frac{2000 y}{57}&\displaystyle - \frac{320 z}{57}\\\displaystyle \frac{40 x}{57}&\displaystyle \frac{80 x}{57} - \frac{80 z}{57}&\displaystyle - \frac{40 z}{57}\\\displaystyle \frac{320 x}{57}&\displaystyle - \frac{2000 y}{57}&\displaystyle \frac{640 x}{57} + \frac{2840 y}{57} + \frac{240 z}{19} - \frac{280}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
\(\displaystyle l_{33}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{ccc}\displaystyle - \frac{s_{1}}{3}&\displaystyle s_{1}&\displaystyle 0\\\displaystyle 0&\displaystyle \frac{2 s_{1}}{3}&\displaystyle 0\\\displaystyle 0&\displaystyle s_{1}&\displaystyle - \frac{s_{1}}{3}\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{33} = \left(\begin{array}{ccc}\displaystyle - \frac{1200 x}{133} - \frac{760 y}{21} - \frac{2960 z}{399} + \frac{200}{19}&\displaystyle \frac{880 y}{21}&\displaystyle - \frac{1480 z}{399}\\\displaystyle \frac{1040 x}{399}&\displaystyle \frac{2080 x}{399} + \frac{3000 y}{133} + \frac{80 z}{21} - \frac{120}{19}&\displaystyle \frac{40 z}{21}\\\displaystyle \frac{40 x}{21}&\displaystyle \frac{2720 y}{399}&\displaystyle \frac{80 x}{21} + \frac{5440 y}{399} + \frac{480 z}{133} - \frac{80}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{33} = \left(\begin{array}{ccc}\displaystyle - \frac{1200 x}{133} - \frac{760 y}{21} - \frac{2960 z}{399} + \frac{200}{19}&\displaystyle \frac{880 y}{21}&\displaystyle - \frac{1480 z}{399}\\\displaystyle \frac{1040 x}{399}&\displaystyle \frac{2080 x}{399} + \frac{3000 y}{133} + \frac{80 z}{21} - \frac{120}{19}&\displaystyle \frac{40 z}{21}\\\displaystyle \frac{40 x}{21}&\displaystyle \frac{2720 y}{399}&\displaystyle \frac{80 x}{21} + \frac{5440 y}{399} + \frac{480 z}{133} - \frac{80}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
\(\displaystyle l_{34}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{ccc}\displaystyle \frac{s_{2}}{3}&\displaystyle 0&\displaystyle - s_{2}\\\displaystyle 0&\displaystyle \frac{s_{2}}{3}&\displaystyle - s_{2}\\\displaystyle 0&\displaystyle 0&\displaystyle - \frac{2 s_{2}}{3}\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{34} = \left(\begin{array}{ccc}\displaystyle - \frac{480 x}{133} - \frac{80 y}{21} - \frac{5440 z}{399} + \frac{80}{19}&\displaystyle - \frac{40 y}{21}&\displaystyle - \frac{2720 z}{399}\\\displaystyle \frac{1480 x}{399}&\displaystyle \frac{2960 x}{399} + \frac{1200 y}{133} + \frac{760 z}{21} - \frac{200}{19}&\displaystyle - \frac{880 z}{21}\\\displaystyle - \frac{40 x}{21}&\displaystyle - \frac{1040 y}{399}&\displaystyle - \frac{80 x}{21} - \frac{2080 y}{399} - \frac{3000 z}{133} + \frac{120}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{34} = \left(\begin{array}{ccc}\displaystyle - \frac{480 x}{133} - \frac{80 y}{21} - \frac{5440 z}{399} + \frac{80}{19}&\displaystyle - \frac{40 y}{21}&\displaystyle - \frac{2720 z}{399}\\\displaystyle \frac{1480 x}{399}&\displaystyle \frac{2960 x}{399} + \frac{1200 y}{133} + \frac{760 z}{21} - \frac{200}{19}&\displaystyle - \frac{880 z}{21}\\\displaystyle - \frac{40 x}{21}&\displaystyle - \frac{1040 y}{399}&\displaystyle - \frac{80 x}{21} - \frac{2080 y}{399} - \frac{3000 z}{133} + \frac{120}{19}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
\(\displaystyle l_{35}:v\mapsto\displaystyle\int_{R}(\left(\begin{array}{ccc}\displaystyle - \frac{2 s_{2}}{3}&\displaystyle 0&\displaystyle s_{2}\\\displaystyle 0&\displaystyle \frac{s_{2}}{3}&\displaystyle 0\\\displaystyle 0&\displaystyle 0&\displaystyle \frac{s_{2}}{3}\end{array}\right))v\)
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{35} = \left(\begin{array}{ccc}\displaystyle - \frac{240 x}{19} - \frac{640 y}{57} - \frac{2840 z}{57} + \frac{280}{19}&\displaystyle - \frac{320 y}{57}&\displaystyle \frac{2000 z}{57}\\\displaystyle \frac{320 x}{57}&\displaystyle \frac{640 x}{57} + \frac{240 y}{19} + \frac{2840 z}{57} - \frac{280}{19}&\displaystyle - \frac{2000 z}{57}\\\displaystyle \frac{40 x}{57}&\displaystyle - \frac{40 y}{57}&\displaystyle \frac{80 x}{57} - \frac{80 y}{57}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.
where \(R\) is the reference element;
and \(s_{0},s_{1},s_{2}\) is a parametrisation of \(R\).
\(\displaystyle \mathbf{\Phi}_{35} = \left(\begin{array}{ccc}\displaystyle - \frac{240 x}{19} - \frac{640 y}{57} - \frac{2840 z}{57} + \frac{280}{19}&\displaystyle - \frac{320 y}{57}&\displaystyle \frac{2000 z}{57}\\\displaystyle \frac{320 x}{57}&\displaystyle \frac{640 x}{57} + \frac{240 y}{19} + \frac{2840 z}{57} - \frac{280}{19}&\displaystyle - \frac{2000 z}{57}\\\displaystyle \frac{40 x}{57}&\displaystyle - \frac{40 y}{57}&\displaystyle \frac{80 x}{57} - \frac{80 y}{57}\end{array}\right)\)
This DOF is associated with volume 0 of the reference element.