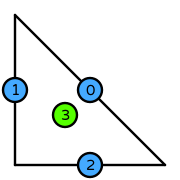
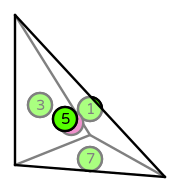
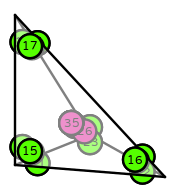
Click here to read what the information on this page means.
| Degrees | \(0\leqslant k\)
where \(k\) is the polynomial subdegree |
| Polynomial subdegree | \(k\) |
| Polynomial superdegree | \(k\) |
| Reference cells | triangle |
| Finite dimensional space | \(\mathcal{P}_{k}^{d\times d}\)
↓ Show set definitions ↓↑ Hide set definitions ↑\(\mathcal{P}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle|\sum_{i=1}^dp_i\leqslant k\right\}\) |
| DOFs | On each facet: integral moments of inner products of tangent(s) and normal to facet with a degree \(k\) Lagrange space
On the interior of the reference cell: integral moments of matrix trace with a degree \(k\) Lagrange space, and integral moments of tensor products against zero normal-tangent trace bubble with a degree \(k-1\) Lagrange space |
| Number of DOFs | triangle: \(2(k+1)(k+2)\) (A046092)
tetrahedron: \(3(k+1)(k+2)(k+3)/2\) |
| Mapping | covariant-contravariant Piola |
| continuity | Tangent-normal inner products on facets are continuous |
| Categories | Matrix-valued elements |
This element is implemented in
FIAT and
Symfem .
↓ Show implementation detail ↓↑ Hide implementation detail ↑| FIAT | FIAT.GopalakrishnanLedererSchoberlFirstKind
↓ Show FIAT examples ↓↑ Hide FIAT examples ↑Before running this example, you must install FIAT: pip3 install git+https://github.com/firedrakeproject/fiat.git This element can then be created with the following lines of Python: import FIAT
# Create Gopalakrishnan-Lederer-Schoberl degree 0
element = FIAT.GopalakrishnanLedererSchoberlFirstKind(FIAT.ufc_cell("triangle"), 1)
# Create Gopalakrishnan-Lederer-Schoberl degree 1
element = FIAT.GopalakrishnanLedererSchoberlFirstKind(FIAT.ufc_cell("triangle"), 2)
# Create Gopalakrishnan-Lederer-Schoberl degree 2
element = FIAT.GopalakrishnanLedererSchoberlFirstKind(FIAT.ufc_cell("triangle"), 3)
# Create Gopalakrishnan-Lederer-Schoberl degree 0
element = FIAT.GopalakrishnanLedererSchoberlFirstKind(FIAT.ufc_cell("tetrahedron"), 1)
# Create Gopalakrishnan-Lederer-Schoberl degree 1
element = FIAT.GopalakrishnanLedererSchoberlFirstKind(FIAT.ufc_cell("tetrahedron"), 2) Note: This implementation uses an alternative value of degree for this element |
| Symfem | "Gopalakrishnan-Lederer-Schoberl"
↓ Show Symfem examples ↓↑ Hide Symfem examples ↑Before running this example, you must install Symfem: pip3 install symfem This element can then be created with the following lines of Python: import symfem
# Create Gopalakrishnan-Lederer-Schoberl degree 0 on a triangle
element = symfem.create_element("triangle", "Gopalakrishnan-Lederer-Schoberl", 0)
# Create Gopalakrishnan-Lederer-Schoberl degree 1 on a triangle
element = symfem.create_element("triangle", "Gopalakrishnan-Lederer-Schoberl", 1)
# Create Gopalakrishnan-Lederer-Schoberl degree 2 on a triangle
element = symfem.create_element("triangle", "Gopalakrishnan-Lederer-Schoberl", 2)
# Create Gopalakrishnan-Lederer-Schoberl degree 0 on a tetrahedron
element = symfem.create_element("tetrahedron", "Gopalakrishnan-Lederer-Schoberl", 0)
# Create Gopalakrishnan-Lederer-Schoberl degree 1 on a tetrahedron
element = symfem.create_element("tetrahedron", "Gopalakrishnan-Lederer-Schoberl", 1) |
- Gopalakrishnan, Jay, Lederer, Philip L., and Schöberl, Joachim. A mass conserving mixed stress formulation for Stokes flow with weakly imposed stress symmetry, SIAM Journal on Numerical Analysis 58(1), 706–732, 2020. [DOI: 10.1137/19M1248960] [BibTeX]
| Element added | 08 April 2025 |
| Element last updated | 04 June 2025 |
