Degree 1 Guzmán–Neilan (second kind) on a tetrahedron

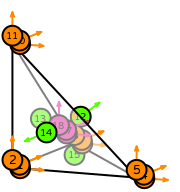
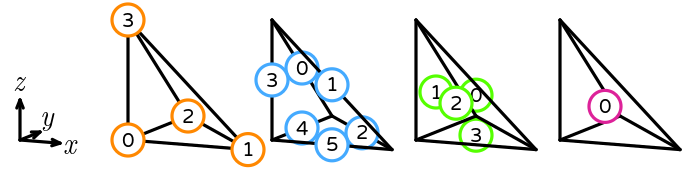
• \(R\) is the reference tetrahedron. The following numbering of the subentities of the reference is used:

• \(\mathcal{V}\) is spanned by: \(\begin{cases} \left(\begin{array}{c}\displaystyle - x - y - 2 z + 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - x - 2 y - z + 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - 2 x - y - z + 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle - x - y - 2 z + 1\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle - x - 2 y - z + 1\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle - 2 x - y - z + 1\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle - x - y - 2 z + 1\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle - x - 2 y - z + 1\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle - 2 x - y - z + 1\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle x - z\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle x - y\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 2 x + y + z - 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle x - z\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle x - y\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 2 x + y + z - 1\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x - z\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x - y\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 2 x + y + z - 1\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle y - z\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - x + y\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle x + 2 y + z - 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle y - z\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle - x + y\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle x + 2 y + z - 1\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle y - z\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle - x + y\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x + 2 y + z - 1\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - y + z\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - x + z\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle x + y + 2 z - 1\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle - y + z\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle - x + z\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle x + y + 2 z - 1\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle - y + z\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle - x + z\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle x + y + 2 z - 1\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle 4 z\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 4 y\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 4 x\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - 4 x - 4 y - 4 z + 4\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle 4 z\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 4 y\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 4 x\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle - 4 x - 4 y - 4 z + 4\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 4 z\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 4 y\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 4 x\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle - 4 x - 4 y - 4 z + 4\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{\sqrt{3} z \left(60 x^{2} + 180 x y + 132 x z - 96 x - 330 y z - 430 z^{2} + 192 z + 9\right)}{180}\\\displaystyle \tfrac{\sqrt{3} z \left(180 x y - 330 x z + 60 y^{2} + 132 y z - 96 y - 430 z^{2} + 192 z + 9\right)}{180}\\\displaystyle \tfrac{\sqrt{3} z \left(- 150 x z - 150 y z - 88 z^{2} + 96 z + 9\right)}{180}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{\sqrt{3} y \left(60 x^{2} + 132 x y + 180 x z - 96 x - 430 y^{2} - 330 y z + 192 y + 9\right)}{180}\\\displaystyle \tfrac{\sqrt{3} y \left(- 150 x y - 88 y^{2} - 150 y z + 96 y + 9\right)}{180}\\\displaystyle \tfrac{\sqrt{3} y \left(- 330 x y + 180 x z - 430 y^{2} + 132 y z + 192 y + 60 z^{2} - 96 z + 9\right)}{180}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{\sqrt{3} x \left(- 88 x^{2} - 150 x y - 150 x z + 96 x + 9\right)}{180}\\\displaystyle \tfrac{\sqrt{3} x \left(- 430 x^{2} + 132 x y - 330 x z + 192 x + 60 y^{2} + 180 y z - 96 y + 9\right)}{180}\\\displaystyle \tfrac{\sqrt{3} x \left(- 430 x^{2} - 330 x y + 132 x z + 192 x + 180 y z + 60 z^{2} - 96 z + 9\right)}{180}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{\sqrt{3} \left(112 x^{3} + 54 x^{2} y + 54 x^{2} z - 156 x^{2} - 168 x y^{2} - 216 x y z + 156 x y - 168 x z^{2} + 156 x z + 3 x - 110 y^{3} - 270 y^{2} z + 252 y^{2} - 270 y z^{2} + 444 y z - 183 y - 110 z^{3} + 252 z^{2} - 183 z + 41\right)}{180}\\\displaystyle \tfrac{\sqrt{3} \left(- 110 x^{3} - 168 x^{2} y - 270 x^{2} z + 252 x^{2} + 54 x y^{2} - 216 x y z + 156 x y - 270 x z^{2} + 444 x z - 183 x + 112 y^{3} + 54 y^{2} z - 156 y^{2} - 168 y z^{2} + 156 y z + 3 y - 110 z^{3} + 252 z^{2} - 183 z + 41\right)}{180}\\\displaystyle \tfrac{\sqrt{3} \left(- 110 x^{3} - 270 x^{2} y - 168 x^{2} z + 252 x^{2} - 270 x y^{2} - 216 x y z + 444 x y + 54 x z^{2} + 156 x z - 183 x - 110 y^{3} - 168 y^{2} z + 252 y^{2} + 54 y z^{2} + 156 y z - 183 y + 112 z^{3} - 156 z^{2} + 3 z + 41\right)}{180}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{z \left(- 90 x y + 216 x z + 12 x - 60 y^{2} + 105 y z + 60 y - 55 z^{2} - 54 z - 3\right)}{60}\\\displaystyle \tfrac{z \left(- 30 y^{2} - 219 y z + 42 y + 325 z^{2} - 69 z - 3\right)}{60}\\\displaystyle \tfrac{z \left(75 y z + z^{2} - 27 z - 3\right)}{60}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{y \left(216 x y - 90 x z + 12 x - 55 y^{2} + 105 y z - 54 y - 60 z^{2} + 60 z - 3\right)}{60}\\\displaystyle \tfrac{y \left(y^{2} + 75 y z - 27 y - 3\right)}{60}\\\displaystyle \tfrac{y \left(325 y^{2} - 219 y z - 69 y - 30 z^{2} + 42 z - 3\right)}{60}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{43 x^{3}}{30} + \tfrac{5 x^{2} y}{4} + \tfrac{5 x^{2} z}{4} - \tfrac{7 x^{2}}{10} - \tfrac{x}{20} - y^{2} z - y z^{2} + y z\\\displaystyle \tfrac{x \left(160 x^{2} - 129 x y + 165 x z - 69 x - 30 y^{2} - 90 y z + 42 y - 3\right)}{60}\\\displaystyle \tfrac{x \left(160 x^{2} + 165 x y - 129 x z - 69 x - 90 y z - 30 z^{2} + 42 z - 3\right)}{60}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{203 x^{3}}{30} + \tfrac{369 x^{2} y}{20} + \tfrac{369 x^{2} z}{20} - \tfrac{173 x^{2}}{10} + \tfrac{161 x y^{2}}{10} + \tfrac{151 x y z}{5} - \tfrac{151 x y}{5} + \tfrac{161 x z^{2}}{10} - \tfrac{151 x z}{5} + \tfrac{283 x}{20} + \tfrac{53 y^{3}}{12} + \tfrac{45 y^{2} z}{4} - \tfrac{62 y^{2}}{5} + \tfrac{45 y z^{2}}{4} - \tfrac{114 y z}{5} + \tfrac{58 y}{5} + \tfrac{53 z^{3}}{12} - \tfrac{62 z^{2}}{5} + \tfrac{58 z}{5} - \tfrac{217}{60}\\\displaystyle - \tfrac{8 x^{3}}{3} - \tfrac{203 x^{2} y}{20} - \tfrac{21 x^{2} z}{4} + \tfrac{137 x^{2}}{20} - \tfrac{59 x y^{2}}{5} - \tfrac{133 x y z}{10} + \tfrac{173 x y}{10} - \tfrac{5 x z^{2}}{2} + \tfrac{41 x z}{5} - \tfrac{113 x}{20} - \tfrac{259 y^{3}}{60} - \tfrac{151 y^{2} z}{20} + \tfrac{199 y^{2}}{20} - \tfrac{63 y z^{2}}{20} + \tfrac{103 y z}{10} - \tfrac{71 y}{10} + \tfrac{z^{3}}{12} + \tfrac{27 z^{2}}{20} - \tfrac{29 z}{10} + \tfrac{22}{15}\\\displaystyle - \tfrac{8 x^{3}}{3} - \tfrac{21 x^{2} y}{4} - \tfrac{203 x^{2} z}{20} + \tfrac{137 x^{2}}{20} - \tfrac{5 x y^{2}}{2} - \tfrac{133 x y z}{10} + \tfrac{41 x y}{5} - \tfrac{59 x z^{2}}{5} + \tfrac{173 x z}{10} - \tfrac{113 x}{20} + \tfrac{y^{3}}{12} - \tfrac{63 y^{2} z}{20} + \tfrac{27 y^{2}}{20} - \tfrac{151 y z^{2}}{20} + \tfrac{103 y z}{10} - \tfrac{29 y}{10} - \tfrac{259 z^{3}}{60} + \tfrac{199 z^{2}}{20} - \tfrac{71 z}{10} + \tfrac{22}{15}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{z \left(30 x^{2} + 219 x z - 42 x - 325 z^{2} + 69 z + 3\right)}{60}\\\displaystyle \tfrac{z \left(60 x^{2} + 90 x y - 105 x z - 60 x - 216 y z - 12 y + 55 z^{2} + 54 z + 3\right)}{60}\\\displaystyle \tfrac{z \left(- 75 x z - z^{2} + 27 z + 3\right)}{60}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{y \left(30 x^{2} + 129 x y + 90 x z - 42 x - 160 y^{2} - 165 y z + 69 y + 3\right)}{60}\\\displaystyle x^{2} z - \tfrac{5 x y^{2}}{4} + x z^{2} - x z - \tfrac{43 y^{3}}{30} - \tfrac{5 y^{2} z}{4} + \tfrac{7 y^{2}}{10} + \tfrac{y}{20}\\\displaystyle \tfrac{y \left(- 165 x y + 90 x z - 160 y^{2} + 129 y z + 69 y + 30 z^{2} - 42 z + 3\right)}{60}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{x \left(- x^{2} - 75 x z + 27 x + 3\right)}{60}\\\displaystyle \tfrac{x \left(55 x^{2} - 216 x y - 105 x z + 54 x + 90 y z - 12 y + 60 z^{2} - 60 z + 3\right)}{60}\\\displaystyle \tfrac{x \left(- 325 x^{2} + 219 x z + 69 x + 30 z^{2} - 42 z + 3\right)}{60}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{259 x^{3}}{60} + \tfrac{59 x^{2} y}{5} + \tfrac{151 x^{2} z}{20} - \tfrac{199 x^{2}}{20} + \tfrac{203 x y^{2}}{20} + \tfrac{133 x y z}{10} - \tfrac{173 x y}{10} + \tfrac{63 x z^{2}}{20} - \tfrac{103 x z}{10} + \tfrac{71 x}{10} + \tfrac{8 y^{3}}{3} + \tfrac{21 y^{2} z}{4} - \tfrac{137 y^{2}}{20} + \tfrac{5 y z^{2}}{2} - \tfrac{41 y z}{5} + \tfrac{113 y}{20} - \tfrac{z^{3}}{12} - \tfrac{27 z^{2}}{20} + \tfrac{29 z}{10} - \tfrac{22}{15}\\\displaystyle - \tfrac{53 x^{3}}{12} - \tfrac{161 x^{2} y}{10} - \tfrac{45 x^{2} z}{4} + \tfrac{62 x^{2}}{5} - \tfrac{369 x y^{2}}{20} - \tfrac{151 x y z}{5} + \tfrac{151 x y}{5} - \tfrac{45 x z^{2}}{4} + \tfrac{114 x z}{5} - \tfrac{58 x}{5} - \tfrac{203 y^{3}}{30} - \tfrac{369 y^{2} z}{20} + \tfrac{173 y^{2}}{10} - \tfrac{161 y z^{2}}{10} + \tfrac{151 y z}{5} - \tfrac{283 y}{20} - \tfrac{53 z^{3}}{12} + \tfrac{62 z^{2}}{5} - \tfrac{58 z}{5} + \tfrac{217}{60}\\\displaystyle - \tfrac{x^{3}}{12} + \tfrac{5 x^{2} y}{2} + \tfrac{63 x^{2} z}{20} - \tfrac{27 x^{2}}{20} + \tfrac{21 x y^{2}}{4} + \tfrac{133 x y z}{10} - \tfrac{41 x y}{5} + \tfrac{151 x z^{2}}{20} - \tfrac{103 x z}{10} + \tfrac{29 x}{10} + \tfrac{8 y^{3}}{3} + \tfrac{203 y^{2} z}{20} - \tfrac{137 y^{2}}{20} + \tfrac{59 y z^{2}}{5} - \tfrac{173 y z}{10} + \tfrac{113 y}{20} + \tfrac{259 z^{3}}{60} - \tfrac{199 z^{2}}{20} + \tfrac{71 z}{10} - \tfrac{22}{15}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\), \(\begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{z \left(- 30 x^{2} - 90 x y - 129 x z + 42 x + 165 y z + 160 z^{2} - 69 z - 3\right)}{60}\\\displaystyle \tfrac{z \left(- 90 x y + 165 x z - 30 y^{2} - 129 y z + 42 y + 160 z^{2} - 69 z - 3\right)}{60}\\\displaystyle - x^{2} y - x y^{2} + x y + \tfrac{5 x z^{2}}{4} + \tfrac{5 y z^{2}}{4} + \tfrac{43 z^{3}}{30} - \tfrac{7 z^{2}}{10} - \tfrac{z}{20}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{y \left(- 30 x^{2} - 219 x y + 42 x + 325 y^{2} - 69 y - 3\right)}{60}\\\displaystyle \tfrac{y \left(75 x y + y^{2} - 27 y - 3\right)}{60}\\\displaystyle \tfrac{y \left(- 60 x^{2} + 105 x y - 90 x z + 60 x - 55 y^{2} + 216 y z - 54 y + 12 z - 3\right)}{60}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{x \left(x^{2} + 75 x y - 27 x - 3\right)}{60}\\\displaystyle \tfrac{x \left(325 x^{2} - 219 x y - 69 x - 30 y^{2} + 42 y - 3\right)}{60}\\\displaystyle \tfrac{x \left(- 55 x^{2} + 105 x y + 216 x z - 54 x - 60 y^{2} - 90 y z + 60 y + 12 z - 3\right)}{60}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - \tfrac{259 x^{3}}{60} - \tfrac{151 x^{2} y}{20} - \tfrac{59 x^{2} z}{5} + \tfrac{199 x^{2}}{20} - \tfrac{63 x y^{2}}{20} - \tfrac{133 x y z}{10} + \tfrac{103 x y}{10} - \tfrac{203 x z^{2}}{20} + \tfrac{173 x z}{10} - \tfrac{71 x}{10} + \tfrac{y^{3}}{12} - \tfrac{5 y^{2} z}{2} + \tfrac{27 y^{2}}{20} - \tfrac{21 y z^{2}}{4} + \tfrac{41 y z}{5} - \tfrac{29 y}{10} - \tfrac{8 z^{3}}{3} + \tfrac{137 z^{2}}{20} - \tfrac{113 z}{20} + \tfrac{22}{15}\\\displaystyle \tfrac{x^{3}}{12} - \tfrac{63 x^{2} y}{20} - \tfrac{5 x^{2} z}{2} + \tfrac{27 x^{2}}{20} - \tfrac{151 x y^{2}}{20} - \tfrac{133 x y z}{10} + \tfrac{103 x y}{10} - \tfrac{21 x z^{2}}{4} + \tfrac{41 x z}{5} - \tfrac{29 x}{10} - \tfrac{259 y^{3}}{60} - \tfrac{59 y^{2} z}{5} + \tfrac{199 y^{2}}{20} - \tfrac{203 y z^{2}}{20} + \tfrac{173 y z}{10} - \tfrac{71 y}{10} - \tfrac{8 z^{3}}{3} + \tfrac{137 z^{2}}{20} - \tfrac{113 z}{20} + \tfrac{22}{15}\\\displaystyle \tfrac{53 x^{3}}{12} + \tfrac{45 x^{2} y}{4} + \tfrac{161 x^{2} z}{10} - \tfrac{62 x^{2}}{5} + \tfrac{45 x y^{2}}{4} + \tfrac{151 x y z}{5} - \tfrac{114 x y}{5} + \tfrac{369 x z^{2}}{20} - \tfrac{151 x z}{5} + \tfrac{58 x}{5} + \tfrac{53 y^{3}}{12} + \tfrac{161 y^{2} z}{10} - \tfrac{62 y^{2}}{5} + \tfrac{369 y z^{2}}{20} - \tfrac{151 y z}{5} + \tfrac{58 y}{5} + \tfrac{203 z^{3}}{30} - \tfrac{173 z^{2}}{10} + \tfrac{283 z}{20} - \tfrac{217}{60}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)
• \(\mathcal{L}=\{l_0,...,l_{18}\}\)
• Functionals and basis functions:

\(\displaystyle l_{0}:\boldsymbol{v}\mapsto\boldsymbol{v}(0,0,0)\cdot\left(\begin{array}{c}1\\0\\0\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{0} = \begin{cases} \left(\begin{array}{c}\displaystyle 30 x y z - 72 x z^{2} - 4 x z - x + 20 y^{2} z - 35 y z^{2} - 20 y z - y + \tfrac{55 z^{3}}{3} + 18 z^{2} + \tfrac{23 z}{12} + 1\\\displaystyle \tfrac{z \left(30 y^{2} + 219 y z - 42 y - 325 z^{2} + 69 z - 2\right)}{3}\\\displaystyle \tfrac{z \left(- 75 y z - z^{2} + 27 z - 2\right)}{3}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - 72 x y^{2} + 30 x y z - 4 x y - x + \tfrac{55 y^{3}}{3} - 35 y^{2} z + 18 y^{2} + 20 y z^{2} - 20 y z + \tfrac{23 y}{12} - z + 1\\\displaystyle \tfrac{y \left(- y^{2} - 75 y z + 27 y - 2\right)}{3}\\\displaystyle \tfrac{y \left(- 325 y^{2} + 219 y z + 69 y + 30 z^{2} - 42 z - 2\right)}{3}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - \tfrac{86 x^{3}}{3} - 25 x^{2} y - 25 x^{2} z + 14 x^{2} + \tfrac{23 x}{12} + 20 y^{2} z + 20 y z^{2} - 20 y z - y - z + 1\\\displaystyle \tfrac{x \left(- 160 x^{2} + 129 x y - 165 x z + 69 x + 30 y^{2} + 90 y z - 42 y - 2\right)}{3}\\\displaystyle \tfrac{x \left(- 160 x^{2} - 165 x y + 129 x z + 69 x + 90 y z + 30 z^{2} - 42 z - 2\right)}{3}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - \tfrac{406 x^{3}}{3} - 369 x^{2} y - 369 x^{2} z + 346 x^{2} - 322 x y^{2} - 604 x y z + 604 x y - 322 x z^{2} + 604 x z - \tfrac{3431 x}{12} - \tfrac{265 y^{3}}{3} - 225 y^{2} z + 248 y^{2} - 225 y z^{2} + 456 y z - \tfrac{2819 y}{12} - \tfrac{265 z^{3}}{3} + 248 z^{2} - \tfrac{2819 z}{12} + \tfrac{301}{4}\\\displaystyle \tfrac{160 x^{3}}{3} + 203 x^{2} y + 105 x^{2} z - 137 x^{2} + 236 x y^{2} + 266 x y z - 346 x y + 50 x z^{2} - 164 x z + \tfrac{344 x}{3} + \tfrac{259 y^{3}}{3} + 151 y^{2} z - 199 y^{2} + 63 y z^{2} - 206 y z + \tfrac{431 y}{3} - \tfrac{5 z^{3}}{3} - 27 z^{2} + \tfrac{179 z}{3} - 31\\\displaystyle \tfrac{160 x^{3}}{3} + 105 x^{2} y + 203 x^{2} z - 137 x^{2} + 50 x y^{2} + 266 x y z - 164 x y + 236 x z^{2} - 346 x z + \tfrac{344 x}{3} - \tfrac{5 y^{3}}{3} + 63 y^{2} z - 27 y^{2} + 151 y z^{2} - 206 y z + \tfrac{179 y}{3} + \tfrac{259 z^{3}}{3} - 199 z^{2} + \tfrac{431 z}{3} - 31\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with vertex 0 of the reference element.

\(\displaystyle l_{1}:\boldsymbol{v}\mapsto\boldsymbol{v}(0,0,0)\cdot\left(\begin{array}{c}0\\1\\0\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{1} = \begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{z \left(30 x^{2} + 219 x z - 42 x - 325 z^{2} + 69 z - 2\right)}{3}\\\displaystyle 20 x^{2} z + 30 x y z - 35 x z^{2} - 20 x z - x - 72 y z^{2} - 4 y z - y + \tfrac{55 z^{3}}{3} + 18 z^{2} + \tfrac{23 z}{12} + 1\\\displaystyle \tfrac{z \left(- 75 x z - z^{2} + 27 z - 2\right)}{3}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{y \left(30 x^{2} + 129 x y + 90 x z - 42 x - 160 y^{2} - 165 y z + 69 y - 2\right)}{3}\\\displaystyle 20 x^{2} z - 25 x y^{2} + 20 x z^{2} - 20 x z - x - \tfrac{86 y^{3}}{3} - 25 y^{2} z + 14 y^{2} + \tfrac{23 y}{12} - z + 1\\\displaystyle \tfrac{y \left(- 165 x y + 90 x z - 160 y^{2} + 129 y z + 69 y + 30 z^{2} - 42 z - 2\right)}{3}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{x \left(- x^{2} - 75 x z + 27 x - 2\right)}{3}\\\displaystyle \tfrac{55 x^{3}}{3} - 72 x^{2} y - 35 x^{2} z + 18 x^{2} + 30 x y z - 4 x y + 20 x z^{2} - 20 x z + \tfrac{23 x}{12} - y - z + 1\\\displaystyle \tfrac{x \left(- 325 x^{2} + 219 x z + 69 x + 30 z^{2} - 42 z - 2\right)}{3}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{259 x^{3}}{3} + 236 x^{2} y + 151 x^{2} z - 199 x^{2} + 203 x y^{2} + 266 x y z - 346 x y + 63 x z^{2} - 206 x z + \tfrac{431 x}{3} + \tfrac{160 y^{3}}{3} + 105 y^{2} z - 137 y^{2} + 50 y z^{2} - 164 y z + \tfrac{344 y}{3} - \tfrac{5 z^{3}}{3} - 27 z^{2} + \tfrac{179 z}{3} - 31\\\displaystyle - \tfrac{265 x^{3}}{3} - 322 x^{2} y - 225 x^{2} z + 248 x^{2} - 369 x y^{2} - 604 x y z + 604 x y - 225 x z^{2} + 456 x z - \tfrac{2819 x}{12} - \tfrac{406 y^{3}}{3} - 369 y^{2} z + 346 y^{2} - 322 y z^{2} + 604 y z - \tfrac{3431 y}{12} - \tfrac{265 z^{3}}{3} + 248 z^{2} - \tfrac{2819 z}{12} + \tfrac{301}{4}\\\displaystyle - \tfrac{5 x^{3}}{3} + 50 x^{2} y + 63 x^{2} z - 27 x^{2} + 105 x y^{2} + 266 x y z - 164 x y + 151 x z^{2} - 206 x z + \tfrac{179 x}{3} + \tfrac{160 y^{3}}{3} + 203 y^{2} z - 137 y^{2} + 236 y z^{2} - 346 y z + \tfrac{344 y}{3} + \tfrac{259 z^{3}}{3} - 199 z^{2} + \tfrac{431 z}{3} - 31\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with vertex 0 of the reference element.

\(\displaystyle l_{2}:\boldsymbol{v}\mapsto\boldsymbol{v}(0,0,0)\cdot\left(\begin{array}{c}0\\0\\1\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{2} = \begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{z \left(30 x^{2} + 90 x y + 129 x z - 42 x - 165 y z - 160 z^{2} + 69 z - 2\right)}{3}\\\displaystyle \tfrac{z \left(90 x y - 165 x z + 30 y^{2} + 129 y z - 42 y - 160 z^{2} + 69 z - 2\right)}{3}\\\displaystyle 20 x^{2} y + 20 x y^{2} - 20 x y - 25 x z^{2} - x - 25 y z^{2} - y - \tfrac{86 z^{3}}{3} + 14 z^{2} + \tfrac{23 z}{12} + 1\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{y \left(30 x^{2} + 219 x y - 42 x - 325 y^{2} + 69 y - 2\right)}{3}\\\displaystyle \tfrac{y \left(- 75 x y - y^{2} + 27 y - 2\right)}{3}\\\displaystyle 20 x^{2} y - 35 x y^{2} + 30 x y z - 20 x y - x + \tfrac{55 y^{3}}{3} - 72 y^{2} z + 18 y^{2} - 4 y z + \tfrac{23 y}{12} - z + 1\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{x \left(- x^{2} - 75 x y + 27 x - 2\right)}{3}\\\displaystyle \tfrac{x \left(- 325 x^{2} + 219 x y + 69 x + 30 y^{2} - 42 y - 2\right)}{3}\\\displaystyle \tfrac{55 x^{3}}{3} - 35 x^{2} y - 72 x^{2} z + 18 x^{2} + 20 x y^{2} + 30 x y z - 20 x y - 4 x z + \tfrac{23 x}{12} - y - z + 1\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{259 x^{3}}{3} + 151 x^{2} y + 236 x^{2} z - 199 x^{2} + 63 x y^{2} + 266 x y z - 206 x y + 203 x z^{2} - 346 x z + \tfrac{431 x}{3} - \tfrac{5 y^{3}}{3} + 50 y^{2} z - 27 y^{2} + 105 y z^{2} - 164 y z + \tfrac{179 y}{3} + \tfrac{160 z^{3}}{3} - 137 z^{2} + \tfrac{344 z}{3} - 31\\\displaystyle - \tfrac{5 x^{3}}{3} + 63 x^{2} y + 50 x^{2} z - 27 x^{2} + 151 x y^{2} + 266 x y z - 206 x y + 105 x z^{2} - 164 x z + \tfrac{179 x}{3} + \tfrac{259 y^{3}}{3} + 236 y^{2} z - 199 y^{2} + 203 y z^{2} - 346 y z + \tfrac{431 y}{3} + \tfrac{160 z^{3}}{3} - 137 z^{2} + \tfrac{344 z}{3} - 31\\\displaystyle - \tfrac{265 x^{3}}{3} - 225 x^{2} y - 322 x^{2} z + 248 x^{2} - 225 x y^{2} - 604 x y z + 456 x y - 369 x z^{2} + 604 x z - \tfrac{2819 x}{12} - \tfrac{265 y^{3}}{3} - 322 y^{2} z + 248 y^{2} - 369 y z^{2} + 604 y z - \tfrac{2819 y}{12} - \tfrac{406 z^{3}}{3} + 346 z^{2} - \tfrac{3431 z}{12} + \tfrac{301}{4}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with vertex 0 of the reference element.

\(\displaystyle l_{3}:\boldsymbol{v}\mapsto\boldsymbol{v}(1,0,0)\cdot\left(\begin{array}{c}1\\0\\0\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{3} = \begin{cases} \left(\begin{array}{c}\displaystyle - \tfrac{20 x^{2} z}{3} - 20 x y z - \tfrac{44 x z^{2}}{3} + \tfrac{32 x z}{3} + x + \tfrac{110 y z^{2}}{3} + \tfrac{430 z^{3}}{9} - \tfrac{64 z^{2}}{3} - \tfrac{37 z}{36}\\\displaystyle \tfrac{z \left(- 720 x y + 1320 x z - 240 y^{2} - 528 y z + 384 y + 1720 z^{2} - 768 z - 1\right)}{36}\\\displaystyle \tfrac{z \left(600 x z + 600 y z + 352 z^{2} - 384 z - 1\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - \tfrac{20 x^{2} y}{3} - \tfrac{44 x y^{2}}{3} - 20 x y z + \tfrac{32 x y}{3} + x + \tfrac{430 y^{3}}{9} + \tfrac{110 y^{2} z}{3} - \tfrac{64 y^{2}}{3} - \tfrac{37 y}{36}\\\displaystyle \tfrac{y \left(600 x y + 352 y^{2} + 600 y z - 384 y - 1\right)}{36}\\\displaystyle \tfrac{y \left(1320 x y - 720 x z + 1720 y^{2} - 528 y z - 768 y - 240 z^{2} + 384 z - 1\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{x \left(352 x^{2} + 600 x y + 600 x z - 384 x - 1\right)}{36}\\\displaystyle \tfrac{x \left(1720 x^{2} - 528 x y + 1320 x z - 768 x - 240 y^{2} - 720 y z + 384 y - 1\right)}{36}\\\displaystyle \tfrac{x \left(1720 x^{2} + 1320 x y - 528 x z - 768 x - 720 y z - 240 z^{2} + 384 z - 1\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - \tfrac{112 x^{3}}{9} - 6 x^{2} y - 6 x^{2} z + \tfrac{52 x^{2}}{3} + \tfrac{56 x y^{2}}{3} + 24 x y z - \tfrac{52 x y}{3} + \tfrac{56 x z^{2}}{3} - \tfrac{52 x z}{3} + \tfrac{25 x}{36} + \tfrac{110 y^{3}}{9} + 30 y^{2} z - 28 y^{2} + 30 y z^{2} - \tfrac{148 y z}{3} + \tfrac{733 y}{36} + \tfrac{110 z^{3}}{9} - 28 z^{2} + \tfrac{733 z}{36} - \tfrac{55}{12}\\\displaystyle \tfrac{110 x^{3}}{9} + \tfrac{56 x^{2} y}{3} + 30 x^{2} z - 28 x^{2} - 6 x y^{2} + 24 x y z - \tfrac{52 x y}{3} + 30 x z^{2} - \tfrac{148 x z}{3} + \tfrac{697 x}{36} - \tfrac{112 y^{3}}{9} - 6 y^{2} z + \tfrac{52 y^{2}}{3} + \tfrac{56 y z^{2}}{3} - \tfrac{52 y z}{3} - \tfrac{47 y}{36} + \tfrac{110 z^{3}}{9} - 28 z^{2} + \tfrac{697 z}{36} - \tfrac{43}{12}\\\displaystyle \tfrac{110 x^{3}}{9} + 30 x^{2} y + \tfrac{56 x^{2} z}{3} - 28 x^{2} + 30 x y^{2} + 24 x y z - \tfrac{148 x y}{3} - 6 x z^{2} - \tfrac{52 x z}{3} + \tfrac{697 x}{36} + \tfrac{110 y^{3}}{9} + \tfrac{56 y^{2} z}{3} - 28 y^{2} - 6 y z^{2} - \tfrac{52 y z}{3} + \tfrac{697 y}{36} - \tfrac{112 z^{3}}{9} + \tfrac{52 z^{2}}{3} - \tfrac{47 z}{36} - \tfrac{43}{12}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with vertex 1 of the reference element.

\(\displaystyle l_{4}:\boldsymbol{v}\mapsto\boldsymbol{v}(1,0,0)\cdot\left(\begin{array}{c}0\\1\\0\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{4} = \begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{5 z \left(24 x^{2} - 144 x y + 420 x z - 24 x + 264 y z - 436 z^{2} + 12 z - 5\right)}{36}\\\displaystyle 20 x^{2} z + 10 x y z + \tfrac{5 x z^{2}}{3} - 20 x z + x - \tfrac{20 y^{2} z}{3} - \tfrac{260 y z^{2}}{3} + \tfrac{20 y z}{3} + \tfrac{595 z^{3}}{9} - \tfrac{10 z^{2}}{3} + \tfrac{26 z}{9}\\\displaystyle \tfrac{5 z \left(- 60 x z + 120 y z + 68 z^{2} - 12 z - 5\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{5 y \left(24 x^{2} + 204 x y + 72 x z - 24 x - 40 y^{2} - 132 y z + 12 y - 5\right)}{36}\\\displaystyle 20 x^{2} z - \tfrac{25 x y^{2}}{3} + 20 x z^{2} - 20 x z + x - \tfrac{170 y^{3}}{9} - \tfrac{25 y^{2} z}{3} + \tfrac{10 y^{2}}{3} + \tfrac{26 y}{9}\\\displaystyle \tfrac{5 y \left(- 132 x y + 72 x z - 40 y^{2} + 204 y z + 12 y + 24 z^{2} - 24 z - 5\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{5 x \left(68 x^{2} + 120 x y - 60 x z - 12 x - 5\right)}{36}\\\displaystyle \tfrac{5 x \left(119 x^{2} - 156 x y + 3 x z - 6 x - 12 y^{2} + 18 y z + 12 y + 36 z^{2} - 36 z + 7\right)}{9}\\\displaystyle \tfrac{5 x \left(- 436 x^{2} + 264 x y + 420 x z + 12 x - 144 y z + 24 z^{2} - 24 z - 5\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{665 x^{3}}{9} + 230 x^{2} y + 145 x^{2} z - \tfrac{545 x^{2}}{3} + \tfrac{665 x y^{2}}{3} + 290 x y z - \tfrac{1090 x y}{3} + \tfrac{245 x z^{2}}{3} - \tfrac{670 x z}{3} + \tfrac{5125 x}{36} + \tfrac{590 y^{3}}{9} + 135 y^{2} z - 165 y^{2} + 80 y z^{2} - \tfrac{640 y z}{3} + \tfrac{4825 y}{36} + \tfrac{95 z^{3}}{9} - 55 z^{2} + \tfrac{2845 z}{36} - \tfrac{415}{12}\\\displaystyle - \tfrac{685 x^{3}}{9} - \tfrac{910 x^{2} y}{3} - 195 x^{2} z + 220 x^{2} - 375 x y^{2} - 580 x y z + \tfrac{1760 x y}{3} - 195 x z^{2} + \tfrac{1220 x z}{3} - \tfrac{1922 x}{9} - \tfrac{1330 y^{3}}{9} - 375 y^{2} z + \tfrac{1090 y^{2}}{3} - \tfrac{910 y z^{2}}{3} + \tfrac{1760 y z}{3} - \tfrac{2576 y}{9} - \tfrac{685 z^{3}}{9} + 220 z^{2} - \tfrac{1931 z}{9} + \tfrac{212}{3}\\\displaystyle \tfrac{95 x^{3}}{9} + 80 x^{2} y + \tfrac{245 x^{2} z}{3} - 55 x^{2} + 135 x y^{2} + 290 x y z - \tfrac{640 x y}{3} + 145 x z^{2} - \tfrac{670 x z}{3} + \tfrac{2845 x}{36} + \tfrac{590 y^{3}}{9} + \tfrac{665 y^{2} z}{3} - 165 y^{2} + 230 y z^{2} - \tfrac{1090 y z}{3} + \tfrac{4825 y}{36} + \tfrac{665 z^{3}}{9} - \tfrac{545 z^{2}}{3} + \tfrac{5125 z}{36} - \tfrac{415}{12}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with vertex 1 of the reference element.

\(\displaystyle l_{5}:\boldsymbol{v}\mapsto\boldsymbol{v}(1,0,0)\cdot\left(\begin{array}{c}0\\0\\1\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{5} = \begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{5 z \left(24 x^{2} + 72 x y + 204 x z - 24 x - 132 y z - 40 z^{2} + 12 z - 5\right)}{36}\\\displaystyle \tfrac{5 z \left(72 x y - 132 x z + 24 y^{2} + 204 y z - 24 y - 40 z^{2} + 12 z - 5\right)}{36}\\\displaystyle 20 x^{2} y + 20 x y^{2} - 20 x y - \tfrac{25 x z^{2}}{3} + x - \tfrac{25 y z^{2}}{3} - \tfrac{170 z^{3}}{9} + \tfrac{10 z^{2}}{3} + \tfrac{26 z}{9}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{5 y \left(24 x^{2} + 420 x y - 144 x z - 24 x - 436 y^{2} + 264 y z + 12 y - 5\right)}{36}\\\displaystyle \tfrac{5 y \left(- 60 x y + 68 y^{2} + 120 y z - 12 y - 5\right)}{36}\\\displaystyle 20 x^{2} y + \tfrac{5 x y^{2}}{3} + 10 x y z - 20 x y + x + \tfrac{595 y^{3}}{9} - \tfrac{260 y^{2} z}{3} - \tfrac{10 y^{2}}{3} - \tfrac{20 y z^{2}}{3} + \tfrac{20 y z}{3} + \tfrac{26 y}{9}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{5 x \left(68 x^{2} - 60 x y + 120 x z - 12 x - 5\right)}{36}\\\displaystyle \tfrac{5 x \left(- 436 x^{2} + 420 x y + 264 x z + 12 x + 24 y^{2} - 144 y z - 24 y - 5\right)}{36}\\\displaystyle \tfrac{5 x \left(119 x^{2} + 3 x y - 156 x z - 6 x + 36 y^{2} + 18 y z - 36 y - 12 z^{2} + 12 z + 7\right)}{9}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{665 x^{3}}{9} + 145 x^{2} y + 230 x^{2} z - \tfrac{545 x^{2}}{3} + \tfrac{245 x y^{2}}{3} + 290 x y z - \tfrac{670 x y}{3} + \tfrac{665 x z^{2}}{3} - \tfrac{1090 x z}{3} + \tfrac{5125 x}{36} + \tfrac{95 y^{3}}{9} + 80 y^{2} z - 55 y^{2} + 135 y z^{2} - \tfrac{640 y z}{3} + \tfrac{2845 y}{36} + \tfrac{590 z^{3}}{9} - 165 z^{2} + \tfrac{4825 z}{36} - \tfrac{415}{12}\\\displaystyle \tfrac{95 x^{3}}{9} + \tfrac{245 x^{2} y}{3} + 80 x^{2} z - 55 x^{2} + 145 x y^{2} + 290 x y z - \tfrac{670 x y}{3} + 135 x z^{2} - \tfrac{640 x z}{3} + \tfrac{2845 x}{36} + \tfrac{665 y^{3}}{9} + 230 y^{2} z - \tfrac{545 y^{2}}{3} + \tfrac{665 y z^{2}}{3} - \tfrac{1090 y z}{3} + \tfrac{5125 y}{36} + \tfrac{590 z^{3}}{9} - 165 z^{2} + \tfrac{4825 z}{36} - \tfrac{415}{12}\\\displaystyle - \tfrac{685 x^{3}}{9} - 195 x^{2} y - \tfrac{910 x^{2} z}{3} + 220 x^{2} - 195 x y^{2} - 580 x y z + \tfrac{1220 x y}{3} - 375 x z^{2} + \tfrac{1760 x z}{3} - \tfrac{1922 x}{9} - \tfrac{685 y^{3}}{9} - \tfrac{910 y^{2} z}{3} + 220 y^{2} - 375 y z^{2} + \tfrac{1760 y z}{3} - \tfrac{1931 y}{9} - \tfrac{1330 z^{3}}{9} + \tfrac{1090 z^{2}}{3} - \tfrac{2576 z}{9} + \tfrac{212}{3}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with vertex 1 of the reference element.

\(\displaystyle l_{6}:\boldsymbol{v}\mapsto\boldsymbol{v}(0,1,0)\cdot\left(\begin{array}{c}1\\0\\0\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{6} = \begin{cases} \left(\begin{array}{c}\displaystyle - \tfrac{20 x^{2} z}{3} + 10 x y z - \tfrac{260 x z^{2}}{3} + \tfrac{20 x z}{3} + 20 y^{2} z + \tfrac{5 y z^{2}}{3} - 20 y z + y + \tfrac{595 z^{3}}{9} - \tfrac{10 z^{2}}{3} + \tfrac{26 z}{9}\\\displaystyle \tfrac{5 z \left(- 144 x y + 264 x z + 24 y^{2} + 420 y z - 24 y - 436 z^{2} + 12 z - 5\right)}{36}\\\displaystyle \tfrac{5 z \left(120 x z - 60 y z + 68 z^{2} - 12 z - 5\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{5 y \left(- 12 x^{2} - 156 x y + 18 x z + 12 x + 119 y^{2} + 3 y z - 6 y + 36 z^{2} - 36 z + 7\right)}{9}\\\displaystyle \tfrac{5 y \left(120 x y + 68 y^{2} - 60 y z - 12 y - 5\right)}{36}\\\displaystyle \tfrac{5 y \left(264 x y - 144 x z - 436 y^{2} + 420 y z + 12 y + 24 z^{2} - 24 z - 5\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - \tfrac{170 x^{3}}{9} - \tfrac{25 x^{2} y}{3} - \tfrac{25 x^{2} z}{3} + \tfrac{10 x^{2}}{3} + \tfrac{26 x}{9} + 20 y^{2} z + 20 y z^{2} - 20 y z + y\\\displaystyle \tfrac{5 x \left(- 40 x^{2} + 204 x y - 132 x z + 12 x + 24 y^{2} + 72 y z - 24 y - 5\right)}{36}\\\displaystyle \tfrac{5 x \left(- 40 x^{2} - 132 x y + 204 x z + 12 x + 72 y z + 24 z^{2} - 24 z - 5\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - \tfrac{1330 x^{3}}{9} - 375 x^{2} y - 375 x^{2} z + \tfrac{1090 x^{2}}{3} - \tfrac{910 x y^{2}}{3} - 580 x y z + \tfrac{1760 x y}{3} - \tfrac{910 x z^{2}}{3} + \tfrac{1760 x z}{3} - \tfrac{2576 x}{9} - \tfrac{685 y^{3}}{9} - 195 y^{2} z + 220 y^{2} - 195 y z^{2} + \tfrac{1220 y z}{3} - \tfrac{1922 y}{9} - \tfrac{685 z^{3}}{9} + 220 z^{2} - \tfrac{1931 z}{9} + \tfrac{212}{3}\\\displaystyle \tfrac{590 x^{3}}{9} + \tfrac{665 x^{2} y}{3} + 135 x^{2} z - 165 x^{2} + 230 x y^{2} + 290 x y z - \tfrac{1090 x y}{3} + 80 x z^{2} - \tfrac{640 x z}{3} + \tfrac{4825 x}{36} + \tfrac{665 y^{3}}{9} + 145 y^{2} z - \tfrac{545 y^{2}}{3} + \tfrac{245 y z^{2}}{3} - \tfrac{670 y z}{3} + \tfrac{5125 y}{36} + \tfrac{95 z^{3}}{9} - 55 z^{2} + \tfrac{2845 z}{36} - \tfrac{415}{12}\\\displaystyle \tfrac{590 x^{3}}{9} + 135 x^{2} y + \tfrac{665 x^{2} z}{3} - 165 x^{2} + 80 x y^{2} + 290 x y z - \tfrac{640 x y}{3} + 230 x z^{2} - \tfrac{1090 x z}{3} + \tfrac{4825 x}{36} + \tfrac{95 y^{3}}{9} + \tfrac{245 y^{2} z}{3} - 55 y^{2} + 145 y z^{2} - \tfrac{670 y z}{3} + \tfrac{2845 y}{36} + \tfrac{665 z^{3}}{9} - \tfrac{545 z^{2}}{3} + \tfrac{5125 z}{36} - \tfrac{415}{12}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with vertex 2 of the reference element.

\(\displaystyle l_{7}:\boldsymbol{v}\mapsto\boldsymbol{v}(0,1,0)\cdot\left(\begin{array}{c}0\\1\\0\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{7} = \begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{z \left(- 240 x^{2} - 720 x y - 528 x z + 384 x + 1320 y z + 1720 z^{2} - 768 z - 1\right)}{36}\\\displaystyle - 20 x y z + \tfrac{110 x z^{2}}{3} - \tfrac{20 y^{2} z}{3} - \tfrac{44 y z^{2}}{3} + \tfrac{32 y z}{3} + y + \tfrac{430 z^{3}}{9} - \tfrac{64 z^{2}}{3} - \tfrac{37 z}{36}\\\displaystyle \tfrac{z \left(600 x z + 600 y z + 352 z^{2} - 384 z - 1\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{y \left(- 240 x^{2} - 528 x y - 720 x z + 384 x + 1720 y^{2} + 1320 y z - 768 y - 1\right)}{36}\\\displaystyle \tfrac{y \left(600 x y + 352 y^{2} + 600 y z - 384 y - 1\right)}{36}\\\displaystyle \tfrac{y \left(1320 x y - 720 x z + 1720 y^{2} - 528 y z - 768 y - 240 z^{2} + 384 z - 1\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{x \left(352 x^{2} + 600 x y + 600 x z - 384 x - 1\right)}{36}\\\displaystyle \tfrac{430 x^{3}}{9} - \tfrac{44 x^{2} y}{3} + \tfrac{110 x^{2} z}{3} - \tfrac{64 x^{2}}{3} - \tfrac{20 x y^{2}}{3} - 20 x y z + \tfrac{32 x y}{3} - \tfrac{37 x}{36} + y\\\displaystyle \tfrac{x \left(1720 x^{2} + 1320 x y - 528 x z - 768 x - 720 y z - 240 z^{2} + 384 z - 1\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - \tfrac{112 x^{3}}{9} - 6 x^{2} y - 6 x^{2} z + \tfrac{52 x^{2}}{3} + \tfrac{56 x y^{2}}{3} + 24 x y z - \tfrac{52 x y}{3} + \tfrac{56 x z^{2}}{3} - \tfrac{52 x z}{3} - \tfrac{47 x}{36} + \tfrac{110 y^{3}}{9} + 30 y^{2} z - 28 y^{2} + 30 y z^{2} - \tfrac{148 y z}{3} + \tfrac{697 y}{36} + \tfrac{110 z^{3}}{9} - 28 z^{2} + \tfrac{697 z}{36} - \tfrac{43}{12}\\\displaystyle \tfrac{110 x^{3}}{9} + \tfrac{56 x^{2} y}{3} + 30 x^{2} z - 28 x^{2} - 6 x y^{2} + 24 x y z - \tfrac{52 x y}{3} + 30 x z^{2} - \tfrac{148 x z}{3} + \tfrac{733 x}{36} - \tfrac{112 y^{3}}{9} - 6 y^{2} z + \tfrac{52 y^{2}}{3} + \tfrac{56 y z^{2}}{3} - \tfrac{52 y z}{3} + \tfrac{25 y}{36} + \tfrac{110 z^{3}}{9} - 28 z^{2} + \tfrac{733 z}{36} - \tfrac{55}{12}\\\displaystyle \tfrac{110 x^{3}}{9} + 30 x^{2} y + \tfrac{56 x^{2} z}{3} - 28 x^{2} + 30 x y^{2} + 24 x y z - \tfrac{148 x y}{3} - 6 x z^{2} - \tfrac{52 x z}{3} + \tfrac{697 x}{36} + \tfrac{110 y^{3}}{9} + \tfrac{56 y^{2} z}{3} - 28 y^{2} - 6 y z^{2} - \tfrac{52 y z}{3} + \tfrac{697 y}{36} - \tfrac{112 z^{3}}{9} + \tfrac{52 z^{2}}{3} - \tfrac{47 z}{36} - \tfrac{43}{12}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with vertex 2 of the reference element.

\(\displaystyle l_{8}:\boldsymbol{v}\mapsto\boldsymbol{v}(0,1,0)\cdot\left(\begin{array}{c}0\\0\\1\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{8} = \begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{5 z \left(24 x^{2} + 72 x y + 204 x z - 24 x - 132 y z - 40 z^{2} + 12 z - 5\right)}{36}\\\displaystyle \tfrac{5 z \left(72 x y - 132 x z + 24 y^{2} + 204 y z - 24 y - 40 z^{2} + 12 z - 5\right)}{36}\\\displaystyle 20 x^{2} y + 20 x y^{2} - 20 x y - \tfrac{25 x z^{2}}{3} - \tfrac{25 y z^{2}}{3} + y - \tfrac{170 z^{3}}{9} + \tfrac{10 z^{2}}{3} + \tfrac{26 z}{9}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{5 y \left(24 x^{2} + 420 x y - 144 x z - 24 x - 436 y^{2} + 264 y z + 12 y - 5\right)}{36}\\\displaystyle \tfrac{5 y \left(- 60 x y + 68 y^{2} + 120 y z - 12 y - 5\right)}{36}\\\displaystyle \tfrac{5 y \left(36 x^{2} + 3 x y + 18 x z - 36 x + 119 y^{2} - 156 y z - 6 y - 12 z^{2} + 12 z + 7\right)}{9}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{5 x \left(68 x^{2} - 60 x y + 120 x z - 12 x - 5\right)}{36}\\\displaystyle \tfrac{5 x \left(- 436 x^{2} + 420 x y + 264 x z + 12 x + 24 y^{2} - 144 y z - 24 y - 5\right)}{36}\\\displaystyle \tfrac{595 x^{3}}{9} + \tfrac{5 x^{2} y}{3} - \tfrac{260 x^{2} z}{3} - \tfrac{10 x^{2}}{3} + 20 x y^{2} + 10 x y z - 20 x y - \tfrac{20 x z^{2}}{3} + \tfrac{20 x z}{3} + \tfrac{26 x}{9} + y\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{665 x^{3}}{9} + 145 x^{2} y + 230 x^{2} z - \tfrac{545 x^{2}}{3} + \tfrac{245 x y^{2}}{3} + 290 x y z - \tfrac{670 x y}{3} + \tfrac{665 x z^{2}}{3} - \tfrac{1090 x z}{3} + \tfrac{5125 x}{36} + \tfrac{95 y^{3}}{9} + 80 y^{2} z - 55 y^{2} + 135 y z^{2} - \tfrac{640 y z}{3} + \tfrac{2845 y}{36} + \tfrac{590 z^{3}}{9} - 165 z^{2} + \tfrac{4825 z}{36} - \tfrac{415}{12}\\\displaystyle \tfrac{95 x^{3}}{9} + \tfrac{245 x^{2} y}{3} + 80 x^{2} z - 55 x^{2} + 145 x y^{2} + 290 x y z - \tfrac{670 x y}{3} + 135 x z^{2} - \tfrac{640 x z}{3} + \tfrac{2845 x}{36} + \tfrac{665 y^{3}}{9} + 230 y^{2} z - \tfrac{545 y^{2}}{3} + \tfrac{665 y z^{2}}{3} - \tfrac{1090 y z}{3} + \tfrac{5125 y}{36} + \tfrac{590 z^{3}}{9} - 165 z^{2} + \tfrac{4825 z}{36} - \tfrac{415}{12}\\\displaystyle - \tfrac{685 x^{3}}{9} - 195 x^{2} y - \tfrac{910 x^{2} z}{3} + 220 x^{2} - 195 x y^{2} - 580 x y z + \tfrac{1220 x y}{3} - 375 x z^{2} + \tfrac{1760 x z}{3} - \tfrac{1931 x}{9} - \tfrac{685 y^{3}}{9} - \tfrac{910 y^{2} z}{3} + 220 y^{2} - 375 y z^{2} + \tfrac{1760 y z}{3} - \tfrac{1922 y}{9} - \tfrac{1330 z^{3}}{9} + \tfrac{1090 z^{2}}{3} - \tfrac{2576 z}{9} + \tfrac{212}{3}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with vertex 2 of the reference element.

\(\displaystyle l_{9}:\boldsymbol{v}\mapsto\boldsymbol{v}(0,0,1)\cdot\left(\begin{array}{c}1\\0\\0\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{9} = \begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{5 z \left(- 12 x^{2} + 18 x y - 156 x z + 12 x + 36 y^{2} + 3 y z - 36 y + 119 z^{2} - 6 z + 7\right)}{9}\\\displaystyle \tfrac{5 z \left(- 144 x y + 264 x z + 24 y^{2} + 420 y z - 24 y - 436 z^{2} + 12 z - 5\right)}{36}\\\displaystyle \tfrac{5 z \left(120 x z - 60 y z + 68 z^{2} - 12 z - 5\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - \tfrac{20 x^{2} y}{3} - \tfrac{260 x y^{2}}{3} + 10 x y z + \tfrac{20 x y}{3} + \tfrac{595 y^{3}}{9} + \tfrac{5 y^{2} z}{3} - \tfrac{10 y^{2}}{3} + 20 y z^{2} - 20 y z + \tfrac{26 y}{9} + z\\\displaystyle \tfrac{5 y \left(120 x y + 68 y^{2} - 60 y z - 12 y - 5\right)}{36}\\\displaystyle \tfrac{5 y \left(264 x y - 144 x z - 436 y^{2} + 420 y z + 12 y + 24 z^{2} - 24 z - 5\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - \tfrac{170 x^{3}}{9} - \tfrac{25 x^{2} y}{3} - \tfrac{25 x^{2} z}{3} + \tfrac{10 x^{2}}{3} + \tfrac{26 x}{9} + 20 y^{2} z + 20 y z^{2} - 20 y z + z\\\displaystyle \tfrac{5 x \left(- 40 x^{2} + 204 x y - 132 x z + 12 x + 24 y^{2} + 72 y z - 24 y - 5\right)}{36}\\\displaystyle \tfrac{5 x \left(- 40 x^{2} - 132 x y + 204 x z + 12 x + 72 y z + 24 z^{2} - 24 z - 5\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - \tfrac{1330 x^{3}}{9} - 375 x^{2} y - 375 x^{2} z + \tfrac{1090 x^{2}}{3} - \tfrac{910 x y^{2}}{3} - 580 x y z + \tfrac{1760 x y}{3} - \tfrac{910 x z^{2}}{3} + \tfrac{1760 x z}{3} - \tfrac{2576 x}{9} - \tfrac{685 y^{3}}{9} - 195 y^{2} z + 220 y^{2} - 195 y z^{2} + \tfrac{1220 y z}{3} - \tfrac{1931 y}{9} - \tfrac{685 z^{3}}{9} + 220 z^{2} - \tfrac{1922 z}{9} + \tfrac{212}{3}\\\displaystyle \tfrac{590 x^{3}}{9} + \tfrac{665 x^{2} y}{3} + 135 x^{2} z - 165 x^{2} + 230 x y^{2} + 290 x y z - \tfrac{1090 x y}{3} + 80 x z^{2} - \tfrac{640 x z}{3} + \tfrac{4825 x}{36} + \tfrac{665 y^{3}}{9} + 145 y^{2} z - \tfrac{545 y^{2}}{3} + \tfrac{245 y z^{2}}{3} - \tfrac{670 y z}{3} + \tfrac{5125 y}{36} + \tfrac{95 z^{3}}{9} - 55 z^{2} + \tfrac{2845 z}{36} - \tfrac{415}{12}\\\displaystyle \tfrac{590 x^{3}}{9} + 135 x^{2} y + \tfrac{665 x^{2} z}{3} - 165 x^{2} + 80 x y^{2} + 290 x y z - \tfrac{640 x y}{3} + 230 x z^{2} - \tfrac{1090 x z}{3} + \tfrac{4825 x}{36} + \tfrac{95 y^{3}}{9} + \tfrac{245 y^{2} z}{3} - 55 y^{2} + 145 y z^{2} - \tfrac{670 y z}{3} + \tfrac{2845 y}{36} + \tfrac{665 z^{3}}{9} - \tfrac{545 z^{2}}{3} + \tfrac{5125 z}{36} - \tfrac{415}{12}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with vertex 3 of the reference element.

\(\displaystyle l_{10}:\boldsymbol{v}\mapsto\boldsymbol{v}(0,0,1)\cdot\left(\begin{array}{c}0\\1\\0\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{10} = \begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{5 z \left(24 x^{2} - 144 x y + 420 x z - 24 x + 264 y z - 436 z^{2} + 12 z - 5\right)}{36}\\\displaystyle \tfrac{5 z \left(36 x^{2} + 18 x y + 3 x z - 36 x - 12 y^{2} - 156 y z + 12 y + 119 z^{2} - 6 z + 7\right)}{9}\\\displaystyle \tfrac{5 z \left(- 60 x z + 120 y z + 68 z^{2} - 12 z - 5\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{5 y \left(24 x^{2} + 204 x y + 72 x z - 24 x - 40 y^{2} - 132 y z + 12 y - 5\right)}{36}\\\displaystyle 20 x^{2} z - \tfrac{25 x y^{2}}{3} + 20 x z^{2} - 20 x z - \tfrac{170 y^{3}}{9} - \tfrac{25 y^{2} z}{3} + \tfrac{10 y^{2}}{3} + \tfrac{26 y}{9} + z\\\displaystyle \tfrac{5 y \left(- 132 x y + 72 x z - 40 y^{2} + 204 y z + 12 y + 24 z^{2} - 24 z - 5\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{5 x \left(68 x^{2} + 120 x y - 60 x z - 12 x - 5\right)}{36}\\\displaystyle \tfrac{595 x^{3}}{9} - \tfrac{260 x^{2} y}{3} + \tfrac{5 x^{2} z}{3} - \tfrac{10 x^{2}}{3} - \tfrac{20 x y^{2}}{3} + 10 x y z + \tfrac{20 x y}{3} + 20 x z^{2} - 20 x z + \tfrac{26 x}{9} + z\\\displaystyle \tfrac{5 x \left(- 436 x^{2} + 264 x y + 420 x z + 12 x - 144 y z + 24 z^{2} - 24 z - 5\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{665 x^{3}}{9} + 230 x^{2} y + 145 x^{2} z - \tfrac{545 x^{2}}{3} + \tfrac{665 x y^{2}}{3} + 290 x y z - \tfrac{1090 x y}{3} + \tfrac{245 x z^{2}}{3} - \tfrac{670 x z}{3} + \tfrac{5125 x}{36} + \tfrac{590 y^{3}}{9} + 135 y^{2} z - 165 y^{2} + 80 y z^{2} - \tfrac{640 y z}{3} + \tfrac{4825 y}{36} + \tfrac{95 z^{3}}{9} - 55 z^{2} + \tfrac{2845 z}{36} - \tfrac{415}{12}\\\displaystyle - \tfrac{685 x^{3}}{9} - \tfrac{910 x^{2} y}{3} - 195 x^{2} z + 220 x^{2} - 375 x y^{2} - 580 x y z + \tfrac{1760 x y}{3} - 195 x z^{2} + \tfrac{1220 x z}{3} - \tfrac{1931 x}{9} - \tfrac{1330 y^{3}}{9} - 375 y^{2} z + \tfrac{1090 y^{2}}{3} - \tfrac{910 y z^{2}}{3} + \tfrac{1760 y z}{3} - \tfrac{2576 y}{9} - \tfrac{685 z^{3}}{9} + 220 z^{2} - \tfrac{1922 z}{9} + \tfrac{212}{3}\\\displaystyle \tfrac{95 x^{3}}{9} + 80 x^{2} y + \tfrac{245 x^{2} z}{3} - 55 x^{2} + 135 x y^{2} + 290 x y z - \tfrac{640 x y}{3} + 145 x z^{2} - \tfrac{670 x z}{3} + \tfrac{2845 x}{36} + \tfrac{590 y^{3}}{9} + \tfrac{665 y^{2} z}{3} - 165 y^{2} + 230 y z^{2} - \tfrac{1090 y z}{3} + \tfrac{4825 y}{36} + \tfrac{665 z^{3}}{9} - \tfrac{545 z^{2}}{3} + \tfrac{5125 z}{36} - \tfrac{415}{12}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with vertex 3 of the reference element.

\(\displaystyle l_{11}:\boldsymbol{v}\mapsto\boldsymbol{v}(0,0,1)\cdot\left(\begin{array}{c}0\\0\\1\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{11} = \begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{z \left(- 240 x^{2} - 720 x y - 528 x z + 384 x + 1320 y z + 1720 z^{2} - 768 z - 1\right)}{36}\\\displaystyle \tfrac{z \left(- 720 x y + 1320 x z - 240 y^{2} - 528 y z + 384 y + 1720 z^{2} - 768 z - 1\right)}{36}\\\displaystyle \tfrac{z \left(600 x z + 600 y z + 352 z^{2} - 384 z - 1\right)}{36}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{y \left(- 240 x^{2} - 528 x y - 720 x z + 384 x + 1720 y^{2} + 1320 y z - 768 y - 1\right)}{36}\\\displaystyle \tfrac{y \left(600 x y + 352 y^{2} + 600 y z - 384 y - 1\right)}{36}\\\displaystyle \tfrac{110 x y^{2}}{3} - 20 x y z + \tfrac{430 y^{3}}{9} - \tfrac{44 y^{2} z}{3} - \tfrac{64 y^{2}}{3} - \tfrac{20 y z^{2}}{3} + \tfrac{32 y z}{3} - \tfrac{37 y}{36} + z\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{x \left(352 x^{2} + 600 x y + 600 x z - 384 x - 1\right)}{36}\\\displaystyle \tfrac{x \left(1720 x^{2} - 528 x y + 1320 x z - 768 x - 240 y^{2} - 720 y z + 384 y - 1\right)}{36}\\\displaystyle \tfrac{430 x^{3}}{9} + \tfrac{110 x^{2} y}{3} - \tfrac{44 x^{2} z}{3} - \tfrac{64 x^{2}}{3} - 20 x y z - \tfrac{20 x z^{2}}{3} + \tfrac{32 x z}{3} - \tfrac{37 x}{36} + z\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - \tfrac{112 x^{3}}{9} - 6 x^{2} y - 6 x^{2} z + \tfrac{52 x^{2}}{3} + \tfrac{56 x y^{2}}{3} + 24 x y z - \tfrac{52 x y}{3} + \tfrac{56 x z^{2}}{3} - \tfrac{52 x z}{3} - \tfrac{47 x}{36} + \tfrac{110 y^{3}}{9} + 30 y^{2} z - 28 y^{2} + 30 y z^{2} - \tfrac{148 y z}{3} + \tfrac{697 y}{36} + \tfrac{110 z^{3}}{9} - 28 z^{2} + \tfrac{697 z}{36} - \tfrac{43}{12}\\\displaystyle \tfrac{110 x^{3}}{9} + \tfrac{56 x^{2} y}{3} + 30 x^{2} z - 28 x^{2} - 6 x y^{2} + 24 x y z - \tfrac{52 x y}{3} + 30 x z^{2} - \tfrac{148 x z}{3} + \tfrac{697 x}{36} - \tfrac{112 y^{3}}{9} - 6 y^{2} z + \tfrac{52 y^{2}}{3} + \tfrac{56 y z^{2}}{3} - \tfrac{52 y z}{3} - \tfrac{47 y}{36} + \tfrac{110 z^{3}}{9} - 28 z^{2} + \tfrac{697 z}{36} - \tfrac{43}{12}\\\displaystyle \tfrac{110 x^{3}}{9} + 30 x^{2} y + \tfrac{56 x^{2} z}{3} - 28 x^{2} + 30 x y^{2} + 24 x y z - \tfrac{148 x y}{3} - 6 x z^{2} - \tfrac{52 x z}{3} + \tfrac{733 x}{36} + \tfrac{110 y^{3}}{9} + \tfrac{56 y^{2} z}{3} - 28 y^{2} - 6 y z^{2} - \tfrac{52 y z}{3} + \tfrac{733 y}{36} - \tfrac{112 z^{3}}{9} + \tfrac{52 z^{2}}{3} + \tfrac{25 z}{36} - \tfrac{55}{12}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with vertex 3 of the reference element.

\(\displaystyle l_{12}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{0}}\boldsymbol{v}\cdot(1)\hat{\boldsymbol{n}}_{0}\)
where \(f_{0}\) is the 0th face;
and \(\hat{\boldsymbol{n}}_{0}\) is the normal to facet 0.

\(\displaystyle \boldsymbol{\phi}_{12} = \begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{z \left(240 x^{2} + 720 x y + 528 x z - 384 x - 1320 y z - 1720 z^{2} + 768 z + 1\right)}{6}\\\displaystyle \tfrac{z \left(720 x y - 1320 x z + 240 y^{2} + 528 y z - 384 y - 1720 z^{2} + 768 z + 1\right)}{6}\\\displaystyle \tfrac{z \left(- 600 x z - 600 y z - 352 z^{2} + 384 z + 1\right)}{6}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{y \left(240 x^{2} + 528 x y + 720 x z - 384 x - 1720 y^{2} - 1320 y z + 768 y + 1\right)}{6}\\\displaystyle \tfrac{y \left(- 600 x y - 352 y^{2} - 600 y z + 384 y + 1\right)}{6}\\\displaystyle \tfrac{y \left(- 1320 x y + 720 x z - 1720 y^{2} + 528 y z + 768 y + 240 z^{2} - 384 z + 1\right)}{6}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{x \left(- 352 x^{2} - 600 x y - 600 x z + 384 x + 1\right)}{6}\\\displaystyle \tfrac{x \left(- 1720 x^{2} + 528 x y - 1320 x z + 768 x + 240 y^{2} + 720 y z - 384 y + 1\right)}{6}\\\displaystyle \tfrac{x \left(- 1720 x^{2} - 1320 x y + 528 x z + 768 x + 720 y z + 240 z^{2} - 384 z + 1\right)}{6}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{224 x^{3}}{3} + 36 x^{2} y + 36 x^{2} z - 104 x^{2} - 112 x y^{2} - 144 x y z + 104 x y - 112 x z^{2} + 104 x z + \tfrac{47 x}{6} - \tfrac{220 y^{3}}{3} - 180 y^{2} z + 168 y^{2} - 180 y z^{2} + 296 y z - \tfrac{697 y}{6} - \tfrac{220 z^{3}}{3} + 168 z^{2} - \tfrac{697 z}{6} + \tfrac{43}{2}\\\displaystyle - \tfrac{220 x^{3}}{3} - 112 x^{2} y - 180 x^{2} z + 168 x^{2} + 36 x y^{2} - 144 x y z + 104 x y - 180 x z^{2} + 296 x z - \tfrac{697 x}{6} + \tfrac{224 y^{3}}{3} + 36 y^{2} z - 104 y^{2} - 112 y z^{2} + 104 y z + \tfrac{47 y}{6} - \tfrac{220 z^{3}}{3} + 168 z^{2} - \tfrac{697 z}{6} + \tfrac{43}{2}\\\displaystyle - \tfrac{220 x^{3}}{3} - 180 x^{2} y - 112 x^{2} z + 168 x^{2} - 180 x y^{2} - 144 x y z + 296 x y + 36 x z^{2} + 104 x z - \tfrac{697 x}{6} - \tfrac{220 y^{3}}{3} - 112 y^{2} z + 168 y^{2} + 36 y z^{2} + 104 y z - \tfrac{697 y}{6} + \tfrac{224 z^{3}}{3} - 104 z^{2} + \tfrac{47 z}{6} + \tfrac{43}{2}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with face 0 of the reference element.

\(\displaystyle l_{13}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{1}}\boldsymbol{v}\cdot(1)\hat{\boldsymbol{n}}_{1}\)
where \(f_{1}\) is the 1st face;
and \(\hat{\boldsymbol{n}}_{1}\) is the normal to facet 1.

\(\displaystyle \boldsymbol{\phi}_{13} = \begin{cases} \left(\begin{array}{c}\displaystyle \tfrac{z \left(- 360 x y + 864 x z + 48 x - 240 y^{2} + 420 y z + 240 y - 220 z^{2} - 216 z - 47\right)}{2}\\\displaystyle 2 z \left(- 30 y^{2} - 219 y z + 42 y + 325 z^{2} - 69 z + 2\right)\\\displaystyle 2 z \left(75 y z + z^{2} - 27 z + 2\right)\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle \tfrac{y \left(864 x y - 360 x z + 48 x - 220 y^{2} + 420 y z - 216 y - 240 z^{2} + 240 z - 47\right)}{2}\\\displaystyle 2 y \left(y^{2} + 75 y z - 27 y + 2\right)\\\displaystyle 2 y \left(325 y^{2} - 219 y z - 69 y - 30 z^{2} + 42 z + 2\right)\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 172 x^{3} + 150 x^{2} y + 150 x^{2} z - 84 x^{2} - \tfrac{47 x}{2} - 120 y^{2} z - 120 y z^{2} + 120 y z\\\displaystyle 2 x \left(160 x^{2} - 129 x y + 165 x z - 69 x - 30 y^{2} - 90 y z + 42 y + 2\right)\\\displaystyle 2 x \left(160 x^{2} + 165 x y - 129 x z - 69 x - 90 y z - 30 z^{2} + 42 z + 2\right)\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 812 x^{3} + 2214 x^{2} y + 2214 x^{2} z - 2076 x^{2} + 1932 x y^{2} + 3624 x y z - 3624 x y + 1932 x z^{2} - 3624 x z + \tfrac{3431 x}{2} + 530 y^{3} + 1350 y^{2} z - 1488 y^{2} + 1350 y z^{2} - 2736 y z + \tfrac{2819 y}{2} + 530 z^{3} - 1488 z^{2} + \tfrac{2819 z}{2} - \tfrac{903}{2}\\\displaystyle - 320 x^{3} - 1218 x^{2} y - 630 x^{2} z + 822 x^{2} - 1416 x y^{2} - 1596 x y z + 2076 x y - 300 x z^{2} + 984 x z - 688 x - 518 y^{3} - 906 y^{2} z + 1194 y^{2} - 378 y z^{2} + 1236 y z - 862 y + 10 z^{3} + 162 z^{2} - 358 z + 186\\\displaystyle - 320 x^{3} - 630 x^{2} y - 1218 x^{2} z + 822 x^{2} - 300 x y^{2} - 1596 x y z + 984 x y - 1416 x z^{2} + 2076 x z - 688 x + 10 y^{3} - 378 y^{2} z + 162 y^{2} - 906 y z^{2} + 1236 y z - 358 y - 518 z^{3} + 1194 z^{2} - 862 z + 186\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with face 1 of the reference element.

\(\displaystyle l_{14}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{2}}\boldsymbol{v}\cdot(1)\hat{\boldsymbol{n}}_{2}\)
where \(f_{2}\) is the 2nd face;
and \(\hat{\boldsymbol{n}}_{2}\) is the normal to facet 2.

\(\displaystyle \boldsymbol{\phi}_{14} = \begin{cases} \left(\begin{array}{c}\displaystyle 2 z \left(30 x^{2} + 219 x z - 42 x - 325 z^{2} + 69 z - 2\right)\\\displaystyle \tfrac{z \left(240 x^{2} + 360 x y - 420 x z - 240 x - 864 y z - 48 y + 220 z^{2} + 216 z + 47\right)}{2}\\\displaystyle 2 z \left(- 75 x z - z^{2} + 27 z - 2\right)\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 2 y \left(30 x^{2} + 129 x y + 90 x z - 42 x - 160 y^{2} - 165 y z + 69 y - 2\right)\\\displaystyle 120 x^{2} z - 150 x y^{2} + 120 x z^{2} - 120 x z - 172 y^{3} - 150 y^{2} z + 84 y^{2} + \tfrac{47 y}{2}\\\displaystyle 2 y \left(- 165 x y + 90 x z - 160 y^{2} + 129 y z + 69 y + 30 z^{2} - 42 z - 2\right)\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 2 x \left(- x^{2} - 75 x z + 27 x - 2\right)\\\displaystyle \tfrac{x \left(220 x^{2} - 864 x y - 420 x z + 216 x + 360 y z - 48 y + 240 z^{2} - 240 z + 47\right)}{2}\\\displaystyle 2 x \left(- 325 x^{2} + 219 x z + 69 x + 30 z^{2} - 42 z - 2\right)\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 518 x^{3} + 1416 x^{2} y + 906 x^{2} z - 1194 x^{2} + 1218 x y^{2} + 1596 x y z - 2076 x y + 378 x z^{2} - 1236 x z + 862 x + 320 y^{3} + 630 y^{2} z - 822 y^{2} + 300 y z^{2} - 984 y z + 688 y - 10 z^{3} - 162 z^{2} + 358 z - 186\\\displaystyle - 530 x^{3} - 1932 x^{2} y - 1350 x^{2} z + 1488 x^{2} - 2214 x y^{2} - 3624 x y z + 3624 x y - 1350 x z^{2} + 2736 x z - \tfrac{2819 x}{2} - 812 y^{3} - 2214 y^{2} z + 2076 y^{2} - 1932 y z^{2} + 3624 y z - \tfrac{3431 y}{2} - 530 z^{3} + 1488 z^{2} - \tfrac{2819 z}{2} + \tfrac{903}{2}\\\displaystyle - 10 x^{3} + 300 x^{2} y + 378 x^{2} z - 162 x^{2} + 630 x y^{2} + 1596 x y z - 984 x y + 906 x z^{2} - 1236 x z + 358 x + 320 y^{3} + 1218 y^{2} z - 822 y^{2} + 1416 y z^{2} - 2076 y z + 688 y + 518 z^{3} - 1194 z^{2} + 862 z - 186\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with face 2 of the reference element.

\(\displaystyle l_{15}:\boldsymbol{v}\mapsto\displaystyle\int_{f_{3}}\boldsymbol{v}\cdot(1)\hat{\boldsymbol{n}}_{3}\)
where \(f_{3}\) is the 3rd face;
and \(\hat{\boldsymbol{n}}_{3}\) is the normal to facet 3.

\(\displaystyle \boldsymbol{\phi}_{15} = \begin{cases} \left(\begin{array}{c}\displaystyle 2 z \left(- 30 x^{2} - 90 x y - 129 x z + 42 x + 165 y z + 160 z^{2} - 69 z + 2\right)\\\displaystyle 2 z \left(- 90 x y + 165 x z - 30 y^{2} - 129 y z + 42 y + 160 z^{2} - 69 z + 2\right)\\\displaystyle - 120 x^{2} y - 120 x y^{2} + 120 x y + 150 x z^{2} + 150 y z^{2} + 172 z^{3} - 84 z^{2} - \tfrac{47 z}{2}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 2 y \left(- 30 x^{2} - 219 x y + 42 x + 325 y^{2} - 69 y + 2\right)\\\displaystyle 2 y \left(75 x y + y^{2} - 27 y + 2\right)\\\displaystyle \tfrac{y \left(- 240 x^{2} + 420 x y - 360 x z + 240 x - 220 y^{2} + 864 y z - 216 y + 48 z - 47\right)}{2}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 2 x \left(x^{2} + 75 x y - 27 x + 2\right)\\\displaystyle 2 x \left(325 x^{2} - 219 x y - 69 x - 30 y^{2} + 42 y + 2\right)\\\displaystyle \tfrac{x \left(- 220 x^{2} + 420 x y + 864 x z - 216 x - 240 y^{2} - 360 y z + 240 y + 48 z - 47\right)}{2}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - 518 x^{3} - 906 x^{2} y - 1416 x^{2} z + 1194 x^{2} - 378 x y^{2} - 1596 x y z + 1236 x y - 1218 x z^{2} + 2076 x z - 862 x + 10 y^{3} - 300 y^{2} z + 162 y^{2} - 630 y z^{2} + 984 y z - 358 y - 320 z^{3} + 822 z^{2} - 688 z + 186\\\displaystyle 10 x^{3} - 378 x^{2} y - 300 x^{2} z + 162 x^{2} - 906 x y^{2} - 1596 x y z + 1236 x y - 630 x z^{2} + 984 x z - 358 x - 518 y^{3} - 1416 y^{2} z + 1194 y^{2} - 1218 y z^{2} + 2076 y z - 862 y - 320 z^{3} + 822 z^{2} - 688 z + 186\\\displaystyle 530 x^{3} + 1350 x^{2} y + 1932 x^{2} z - 1488 x^{2} + 1350 x y^{2} + 3624 x y z - 2736 x y + 2214 x z^{2} - 3624 x z + \tfrac{2819 x}{2} + 530 y^{3} + 1932 y^{2} z - 1488 y^{2} + 2214 y z^{2} - 3624 y z + \tfrac{2819 y}{2} + 812 z^{3} - 2076 z^{2} + \tfrac{3431 z}{2} - \tfrac{903}{2}\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with face 3 of the reference element.

\(\displaystyle l_{16}:\boldsymbol{v}\mapsto\boldsymbol{v}(\tfrac{1}{4},\tfrac{1}{4},\tfrac{1}{4})\cdot\left(\begin{array}{c}1\\0\\0\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{16} = \begin{cases} \left(\begin{array}{c}\displaystyle 4 z\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 4 y\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 4 x\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle - 4 x - 4 y - 4 z + 4\\\displaystyle 0\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with volume 0 of the reference element.

\(\displaystyle l_{17}:\boldsymbol{v}\mapsto\boldsymbol{v}(\tfrac{1}{4},\tfrac{1}{4},\tfrac{1}{4})\cdot\left(\begin{array}{c}0\\1\\0\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{17} = \begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle 4 z\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 4 y\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 4 x\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle - 4 x - 4 y - 4 z + 4\\\displaystyle 0\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with volume 0 of the reference element.

\(\displaystyle l_{18}:\boldsymbol{v}\mapsto\boldsymbol{v}(\tfrac{1}{4},\tfrac{1}{4},\tfrac{1}{4})\cdot\left(\begin{array}{c}0\\0\\1\end{array}\right)\)

\(\displaystyle \boldsymbol{\phi}_{18} = \begin{cases} \left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 4 z\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 1, 0), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 4 y\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (1, 0, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle 4 x\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((0, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\\\left(\begin{array}{c}\displaystyle 0\\\displaystyle 0\\\displaystyle - 4 x - 4 y - 4 z + 4\end{array}\right)&\text{in }\operatorname{Tetrahedron}(((1, 0, 0), (0, 1, 0), (0, 0, 1), (1/4, 1/4, 1/4)))\end{cases}\)

This DOF is associated with volume 0 of the reference element.