an encyclopedia of finite element definitions
Guzmán–Neilan (second kind)
Click here to read what the information on this page means.
| Degrees | triangle: \(k=1\) tetrahedron: \(1\leqslant k\leqslant 2\) |
| Reference elements | triangle, tetrahedron |
| DOFs | On each vertex: point evaluations in coordinate directions On each edge: (if \(k>1\)) point evaluations in coordinate directions at midpoints On each facet: normal integral moments with an degree \(0\) Lagrange space On the interior of the reference element: point evaluations in coordinate directions at the midpoint, and (if \(k>1\)) point evaluations in coordinate directions at midpoints of internal edges |
| Number of DOFs | triangle: \(11\) tetrahedron: \(\begin{cases}19&k=1\\49&k=2\end{cases}\) |
| Mapping | contravariant Piola |
| continuity | Function values are continuous. |
| Categories | Vector-valued elements, Macro elements |
Implementations
This element is implemented in FIAT and Symfem .↓ Show implementation detail ↓Examples
| triangle degree 1 | 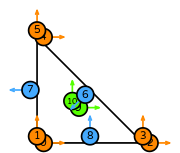 (click to view basis functions) |
| tetrahedron degree 1 | 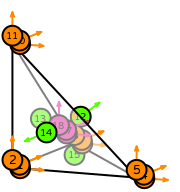 (click to view basis functions) |
| tetrahedron degree 2 |  (click to view basis functions) |
References
- Guzmán, Johnny and Neilan, Michael. Inf-sup stable finite elements on barycentric refinements producing divergence-free approximations in arbitrary dimensions, SIAM Journal on Numerical Analysis 56, 2826–2844, 2018. [DOI: 10.1137/17M1153467] [BibTeX]
DefElement stats
| Element added | 16 October 2024 |
| Element last updated | 16 October 2024 |