an encyclopedia of finite element definitions
Degree 2 Morley on a triangle
◀ Back to Morley definition page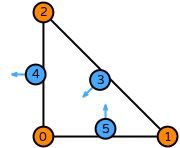
- \(R\) is the reference triangle. The following numbering of the subentities of the reference is used:
- \(\mathcal{V}\) is spanned by: \(1\), \(x\), \(x^{2}\), \(y\), \(x y\), \(y^{2}\)
- \(\mathcal{L}=\{l_0,...,l_{5}\}\)
- Functionals and basis functions:
\(\displaystyle l_{0}:v\mapsto v(0,0)\)
\(\displaystyle \phi_{0} = 2 x y - x - y + 1\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle \phi_{0} = 2 x y - x - y + 1\)
This DOF is associated with vertex 0 of the reference element.
\(\displaystyle l_{1}:v\mapsto v(1,0)\)
\(\displaystyle \phi_{1} = \frac{x^{2}}{2} - x y + \frac{x}{2} - \frac{y^{2}}{2} + \frac{y}{2}\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle \phi_{1} = \frac{x^{2}}{2} - x y + \frac{x}{2} - \frac{y^{2}}{2} + \frac{y}{2}\)
This DOF is associated with vertex 1 of the reference element.
\(\displaystyle l_{2}:v\mapsto v(0,1)\)
\(\displaystyle \phi_{2} = - \frac{x^{2}}{2} - x y + \frac{x}{2} + \frac{y^{2}}{2} + \frac{y}{2}\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle \phi_{2} = - \frac{x^{2}}{2} - x y + \frac{x}{2} + \frac{y^{2}}{2} + \frac{y}{2}\)
This DOF is associated with vertex 2 of the reference element.
\(\displaystyle l_{3}:v\mapsto\nabla {v}(\tfrac{1}{2},\tfrac{1}{2})\cdot\hat{\boldsymbol{n}}_{0}\)
where \(\hat{\boldsymbol{n}}_{0}\) is the normal to facet 0.
\(\displaystyle \phi_{3} = \frac{\sqrt{2} \left(- x^{2} - 2 x y + x - y^{2} + y\right)}{2}\)
This DOF is associated with edge 0 of the reference element.
where \(\hat{\boldsymbol{n}}_{0}\) is the normal to facet 0.
\(\displaystyle \phi_{3} = \frac{\sqrt{2} \left(- x^{2} - 2 x y + x - y^{2} + y\right)}{2}\)
This DOF is associated with edge 0 of the reference element.
\(\displaystyle l_{4}:v\mapsto\nabla {v}(0,\tfrac{1}{2})\cdot\hat{\boldsymbol{n}}_{1}\)
where \(\hat{\boldsymbol{n}}_{1}\) is the normal to facet 1.
\(\displaystyle \phi_{4} = x \left(x - 1\right)\)
This DOF is associated with edge 1 of the reference element.
where \(\hat{\boldsymbol{n}}_{1}\) is the normal to facet 1.
\(\displaystyle \phi_{4} = x \left(x - 1\right)\)
This DOF is associated with edge 1 of the reference element.
\(\displaystyle l_{5}:v\mapsto\nabla {v}(\tfrac{1}{2},0)\cdot\hat{\boldsymbol{n}}_{2}\)
where \(\hat{\boldsymbol{n}}_{2}\) is the normal to facet 2.
\(\displaystyle \phi_{5} = y \left(1 - y\right)\)
This DOF is associated with edge 2 of the reference element.
where \(\hat{\boldsymbol{n}}_{2}\) is the normal to facet 2.
\(\displaystyle \phi_{5} = y \left(1 - y\right)\)
This DOF is associated with edge 2 of the reference element.