Serendipity

Click here to read what the information on this page means.

De Rham complex families	\(\left[S_{1,k}^\square\right]_{0}\) or \(\mathcal{S}_{k}\Lambda^{0}(\square_d)\), \(\left[S_{2,k-d}^\square\right]_{0}\) or \(\mathcal{S}^-_{k-d}\Lambda^{0}(\square_d)\)
Abbreviated names	S
Degrees	\(1\leqslant k\) where \(k\) is the polynomial subdegree
Polynomial subdegree	\(k\)
Polynomial superdegree	\(k + d - 1\)
Lagrange subdegree	\(\max(1,\operatorname{floor}(k/d))\)
Lagrange superdegree	\(k\)
Reference cells	interval, quadrilateral, hexahedron
Finite dimensional space	\(\mathcal{P}_{k} \oplus \mathcal{X}_{k}\) ↓ Show set definitions ↓↑ Hide set definitions ↑ \(\mathcal{P}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle\|\sum_{i=1}^dp_i\leqslant k\right\}\) \(\mathcal{X}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle\|k<\sum_{i=1}^da_i\leqslant k+\#\left\{i\in\{1,\dots,d\}\middle\| a_i=1\right\}\right\}\)
DOFs	On each vertex: point evaluations On each edge: integral moments with a degree \(k-2\) dPc space On each face: integral moments with a degree \(k-4\) dPc space On each volume: integral moments with a degree \(k-6\) dPc space
Number of DOFs	interval: \(k+1\) (A000027) quadrilateral: \(\begin{cases}4&k=1\\(k+1)(k+2)/2+2&k>1\end{cases}\) (A340266) hexahedron: \(\begin{cases}12k-4&k=1,2,3\\3k^2-3k+14&k=4,5\\(k+1)(k+2)(k+3)/6+3k+3&k>6\end{cases}\)
Mapping	identity
continuity	Function values are continuous.
Categories	Scalar-valued elements

Implementations

This element is implemented in Basix , Basix.UFL , Ferrite.jl, FIAT , and Symfem .↓ Show implementation detail ↓

↑ Hide implementation detail ↑

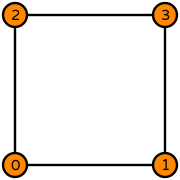
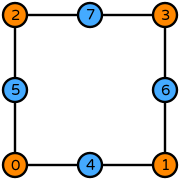
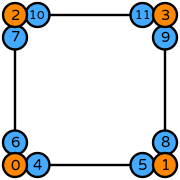
Basix	`basix.ElementFamily.serendipity, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced`↓ Show Basix Python examples ↓↑ Hide Basix Python examples ↑ Before running this example, you must install Basix: pip install fenics-basix This element can then be created with the following lines of Python: import basix # Create serendipity degree 1 on a interval element = basix.create_element(basix.ElementFamily.serendipity, basix.CellType.interval, 1, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) # Create serendipity degree 2 on a interval element = basix.create_element(basix.ElementFamily.serendipity, basix.CellType.interval, 2, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) # Create serendipity degree 3 on a interval element = basix.create_element(basix.ElementFamily.serendipity, basix.CellType.interval, 3, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) # Create serendipity degree 1 on a quadrilateral element = basix.create_element(basix.ElementFamily.serendipity, basix.CellType.quadrilateral, 1, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) # Create serendipity degree 2 on a quadrilateral element = basix.create_element(basix.ElementFamily.serendipity, basix.CellType.quadrilateral, 2, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) # Create serendipity degree 3 on a quadrilateral element = basix.create_element(basix.ElementFamily.serendipity, basix.CellType.quadrilateral, 3, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) This implementation is correct for all the examples below.
Basix.UFL	`basix.ElementFamily.serendipity, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced`↓ Show Basix.UFL Python examples ↓↑ Hide Basix.UFL Python examples ↑ Before running this example, you must install Basix.UFL: pip install fenics-ufl pip install fenics-basix This element can then be created with the following lines of Python: import basix import basix.ufl # Create serendipity degree 1 on a interval element = basix.ufl.element(basix.ElementFamily.serendipity, basix.CellType.interval, 1, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) # Create serendipity degree 2 on a interval element = basix.ufl.element(basix.ElementFamily.serendipity, basix.CellType.interval, 2, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) # Create serendipity degree 3 on a interval element = basix.ufl.element(basix.ElementFamily.serendipity, basix.CellType.interval, 3, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) # Create serendipity degree 1 on a quadrilateral element = basix.ufl.element(basix.ElementFamily.serendipity, basix.CellType.quadrilateral, 1, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) # Create serendipity degree 2 on a quadrilateral element = basix.ufl.element(basix.ElementFamily.serendipity, basix.CellType.quadrilateral, 2, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) # Create serendipity degree 3 on a quadrilateral element = basix.ufl.element(basix.ElementFamily.serendipity, basix.CellType.quadrilateral, 3, lagrange_variant=basix.LagrangeVariant.equispaced, dpc_variant=basix.DPCVariant.simplex_equispaced) This implementation is correct for all the examples below.
Ferrite.jl	`Serendipity`↓ Show Ferrite.jl Julia examples ↓↑ Hide Ferrite.jl Julia examples ↑ Before running this example, you must install Ferrite.jl: julia -e 'using Pkg; Pkg.add("Ferrite")' This element can then be created with the following lines of Julia: using Ferrite # Create serendipity degree 2 on a quadrilateral ip = Serendipity{RefQuadrilateral, 2}() Note: Ferrite.jl uses point evaluations at the midpoints of the edges of the cell in place of the integral moments used in DefElement's definition of this element. Its basis functions therefore differ from the ones shown here, although they span the same space.
FIAT	`FIAT.Serendipity`↓ Show FIAT Python examples ↓↑ Hide FIAT Python examples ↑ Before running this example, you must install FIAT: pip install firedrake-fiat This element can then be created with the following lines of Python: import FIAT # Create serendipity degree 1 on a interval element = FIAT.Serendipity(FIAT.ufc_cell("interval"), 1) # Create serendipity degree 2 on a interval element = FIAT.Serendipity(FIAT.ufc_cell("interval"), 2) # Create serendipity degree 3 on a interval element = FIAT.Serendipity(FIAT.ufc_cell("interval"), 3) # Create serendipity degree 1 on a quadrilateral element = FIAT.Serendipity(FIAT.reference_element.UFCQuadrilateral(), 1) # Create serendipity degree 2 on a quadrilateral element = FIAT.Serendipity(FIAT.reference_element.UFCQuadrilateral(), 2) # Create serendipity degree 3 on a quadrilateral element = FIAT.Serendipity(FIAT.reference_element.UFCQuadrilateral(), 3) This implementation is correct for all the examples below.
Symfem	`"serendipity"`↓ Show Symfem Python examples ↓↑ Hide Symfem Python examples ↑ Before running this example, you must install Symfem: pip install symfem This element can then be created with the following lines of Python: import symfem # Create serendipity degree 1 on a interval element = symfem.create_element("interval", "serendipity", 1) # Create serendipity degree 2 on a interval element = symfem.create_element("interval", "serendipity", 2) # Create serendipity degree 3 on a interval element = symfem.create_element("interval", "serendipity", 3) # Create serendipity degree 1 on a quadrilateral element = symfem.create_element("quadrilateral", "serendipity", 1) # Create serendipity degree 2 on a quadrilateral element = symfem.create_element("quadrilateral", "serendipity", 2) # Create serendipity degree 3 on a quadrilateral element = symfem.create_element("quadrilateral", "serendipity", 3) This implementation is used to compute the examples below and verify other implementations.

Examples

interval degree 1	(click to view basis functions)
interval degree 2	(click to view basis functions)
interval degree 3	(click to view basis functions)
quadrilateral degree 1	(click to view basis functions)
quadrilateral degree 2	(click to view basis functions)
quadrilateral degree 3	(click to view basis functions)

References

[1] Arnold, Douglas N. and Awanou, Gerard. The serendipity family of finite elements, Foundations of Computational Mathematics 11(3), 337–344, 2011. [DOI: 10.1007/s10208-011-9087-3] [BibTeX]
[2] Arnold, Douglas N. and Logg, Anders. Periodic table of the finite elements, SIAM News 47, 2014. [www.siam.org/publications/siam-news/issues/volume-47-number-09-november-2014/] [BibTeX]
[3] Cockburn, Bernardo and Fu, Guosheng. A systematic construction of finite element commuting exact sequences, SIAM journal on numerical analysis 55, 1650–1688, 2017. [DOI: 10.1137/16M1073352] [BibTeX]

DefElement stats

Element added	02 January 2021
Element last updated	06 August 2026