an encyclopedia of finite element definitions

Wu–Xu

Click here to read what the information on this page means.

Degrees	interval: \(k=3\) triangle: \(k=3\) tetrahedron: \(k=4\)
Polynomial subdegree	interval: \(k\) triangle: \(k\) tetrahedron: \(k\)
Polynomial superdegree	\(k\)
Reference cells	interval, triangle, tetrahedron
Finite dimensional space	\(\mathcal{P}_{k}\) (interval) \(\mathcal{P}_{k} \oplus \mathcal{Z}^{(52)}_{1}\) (triangle) \(\mathcal{P}_{k} \oplus \mathcal{Z}^{(53)}_{1}\) (tetrahedron) ↓ Show set definitions ↓↑ Hide set definitions ↑ \(\mathcal{P}_k=\operatorname{span}\left\{\prod_{i=1}^dx_i^{p_i}\middle\|\sum_{i=1}^dp_i\leqslant k\right\}\) \(\mathcal{Z}^{(52)}_k=\left\{xy(1-x-y)p\middle\|p\in\mathcal{P}_{k}\setminus\mathcal{P}_{0}\right\}\) \(\mathcal{Z}^{(53)}_k=\left\{xyz(1-x-y-z)p\middle\|p\in\mathcal{P}_{k}\setminus\mathcal{P}_{0}\right\}\)
DOFs	On each vertex: point evaluations On each edge: integrals of normal derivatives On each face: integrals of normal derivatives On each volume: integrals of normal derivatives
Number of DOFs	interval: \(4\) triangle: \(12\) tetrahedron: \(38\)
Mapping	see [2]
continuity	Function values are continuous.
Notes	This is a higher degree version of the Morley–Wang–Xu element.
Categories	Scalar-valued elements

Implementations

This element is implemented in Symfem .↓ Show implementation detail ↓

Examples

interval degree 3	(click to view basis functions)
triangle degree 3	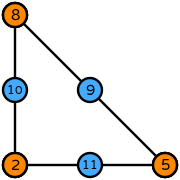(click to view basis functions)
tetrahedron degree 4	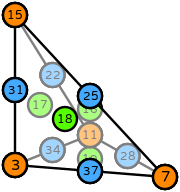(click to view basis functions)

References

[1] Wu, Shuonan and Xu, Jinchao. Nonconforming finite element spaces for 2mth order partial differential equations on Rn simplical grids when m=n+1, Mathematics of computation 88, 531–551, 2019. [DOI: 10.1090/mcom/3361] [BibTeX]
[2] Kirby, Robert C. A general approach to transforming finite elements, The SMAI journal of computational mathematics 4, 197–224, 2018. [DOI: 10.5802/smai-jcm.33] [BibTeX]

DefElement stats

Element added	08 June 2021
Element last updated	20 November 2025